Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-VECTORS-Exercise Multiple Correct
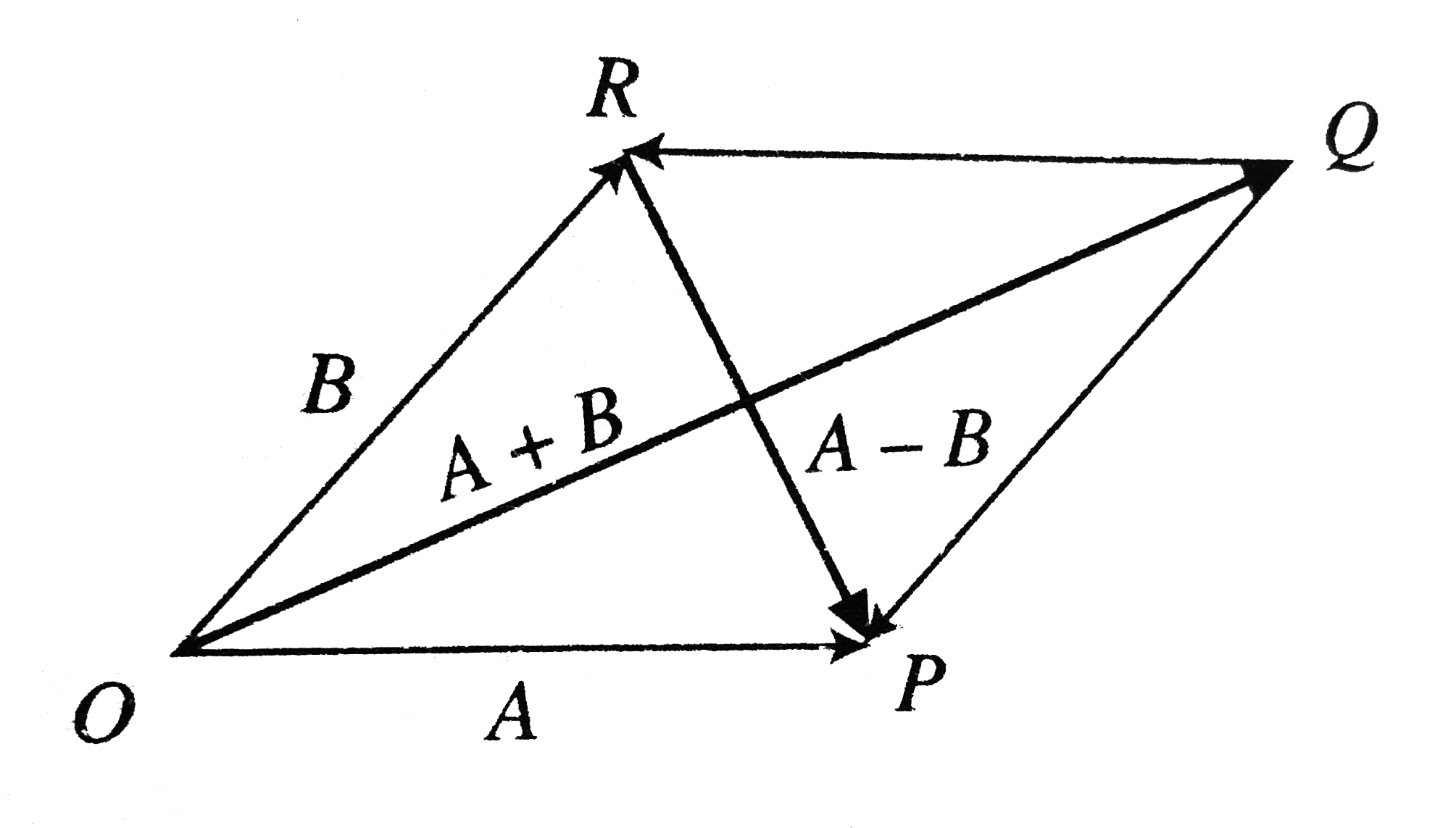
- By vector method, prove that if the diagonals of a parallelogram inter...
Text Solution
|
- Which of the following statements is/ are correct(Figure)
Text Solution
|
- Give two vectors vec(A)==3hat(i)+4hat(j) and vec(B)=hat(i)+hat(j).thet...
Text Solution
|
- If vec(A)=2hat(i)+hat(j)+hat(k) and vec(B)=hat(i)+hat(j)+hat(k) are tw...
Text Solution
|
- If vec(v)(1)+vec(v)(2) is perpendicular to vec(v)(1)-vec(v)(2), then
Text Solution
|
- Two vectors vec(A) and vec(B) lie in plane, another vector vec(C ) lie...
Text Solution
|