Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
VECTORS
CENGAGE PHYSICS|Exercise Exercise Single Correct|51 VideosVECTORS
CENGAGE PHYSICS|Exercise Exercise Multiple Correct|5 VideosVECTORS
CENGAGE PHYSICS|Exercise Exercise 3.2|13 VideosTRAVELLING WAVES
CENGAGE PHYSICS|Exercise Integer|9 VideosWORK, POWER & ENERGY
CENGAGE PHYSICS|Exercise Archives (integer)|4 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-VECTORS-Exercise Subjective
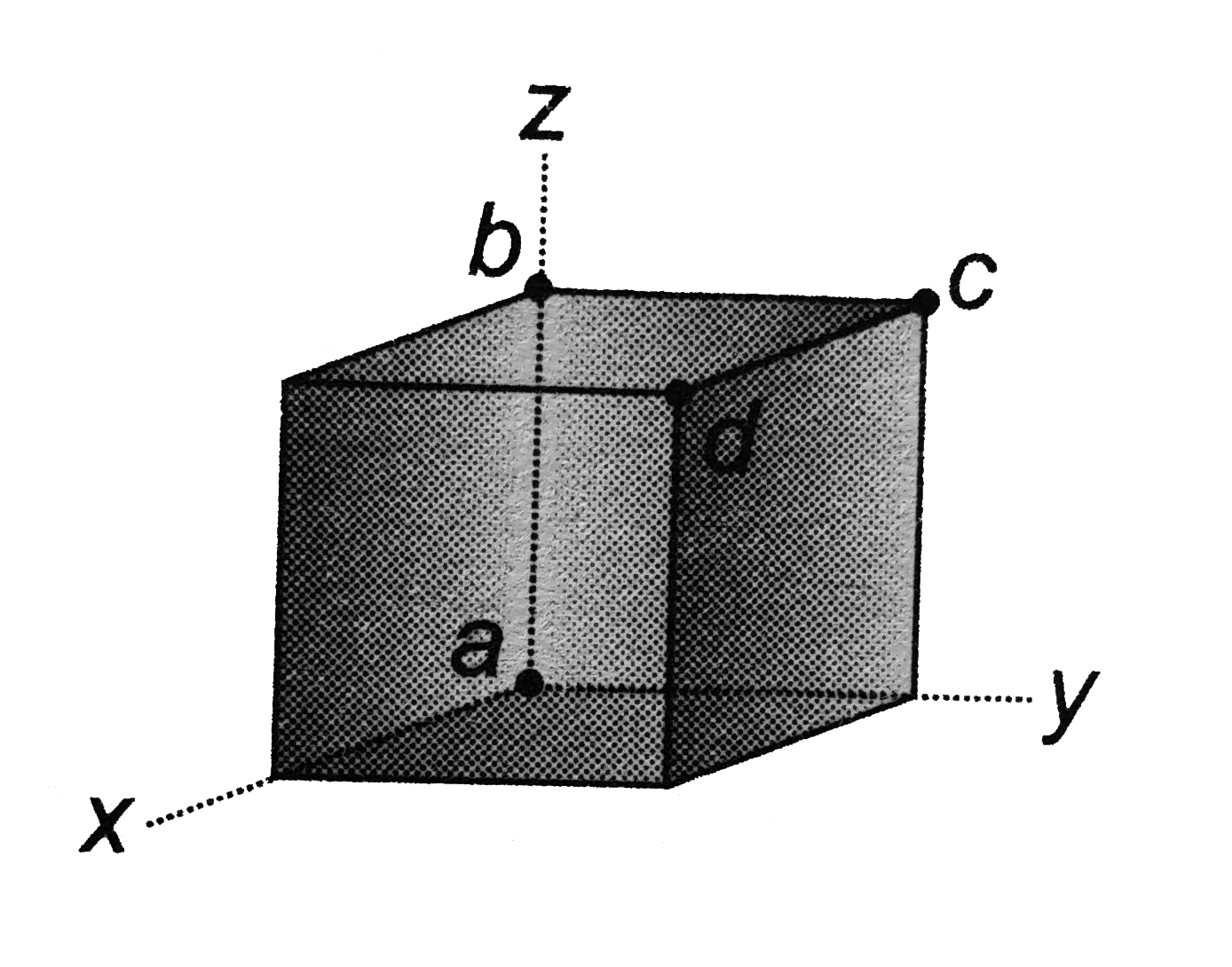
- A cube is placed so that one corner is at the origin and three edges a...
Text Solution
|
- You are given vector vec(A)=5hat(i)-6.5hat(j) and vec(B)=10hat(i)-7hat...
Text Solution
|
- Two vector vec(A) and vec(B) have magnitudes A=3.00 and B=3.00. Their ...
Text Solution
|
- Given two vectors vec(A)=3hat(i)+hat(j)+hat(k) and vec(B)=hat(i)-hat(j...
Text Solution
|
- On a horizontal flat ground, a person is standing at a point A. At thi...
Text Solution
|
- Find the vector sum of N coplanar forces, each of the magnitude F,when...
Text Solution
|
- Can you find at least one vector perpendiculr to 3hat(i)-4hat(j)+7hat(...
Text Solution
|
- Two forces P and Q acting at a point are such that if P is reveserd, t...
Text Solution
|
- Unit vector hat(P) and hat(Q) are inclined at an angle theta. Prove th...
Text Solution
|
- A sail boat sails 2km due east, 5km 37^(@) south of east, and finally ...
Text Solution
|
- Two forces of magnitudes P and Q are inclined at an angle (theta). The...
Text Solution
|
- A vector vec(B) which has a magnitude 8.0 is added to a vector vec(A) ...
Text Solution
|
- Three vector as shown in (figure) have magnitudes |vec(a)|=3,|vec(b)|=...
Text Solution
|
- A bouy is attached to three tugboats by three ropes. The tugboats are ...
Text Solution
|
- Two horizontal forces of magnitudes of 10N and P N act on a particle. ...
Text Solution
|
- The position vectors of two balls are given by vec(r )(1)=2 (m)i+7(m...
Text Solution
|
- A particle whose speed is 50ms^(-1) moves along the line from A(2,1) t...
Text Solution
|
- A particle travels with speed 50ms^(-1) from the point (3,-7) in a dir...
Text Solution
|
- A particle has an initial velocity of 3hat(i) + 4 hat(j) and an accele...
Text Solution
|
- Forces X,Y and Z have magnitudes 10N 5(sqrt(3)-1) N and 5(sqrt(3)+1) N...
Text Solution
|