Since the angle of inclination of the plane is more than the angle of repose i, e `37^(@) gt tan^(-1)0.5` or `tan 37^(@) gt 0.5 ` therefore the block `M` has a tendency to slide down in order to tension in of stationary the neccessury force is applied by the tension in the string
If the block `M` also has the tendency to side down the friction will act in up the plane
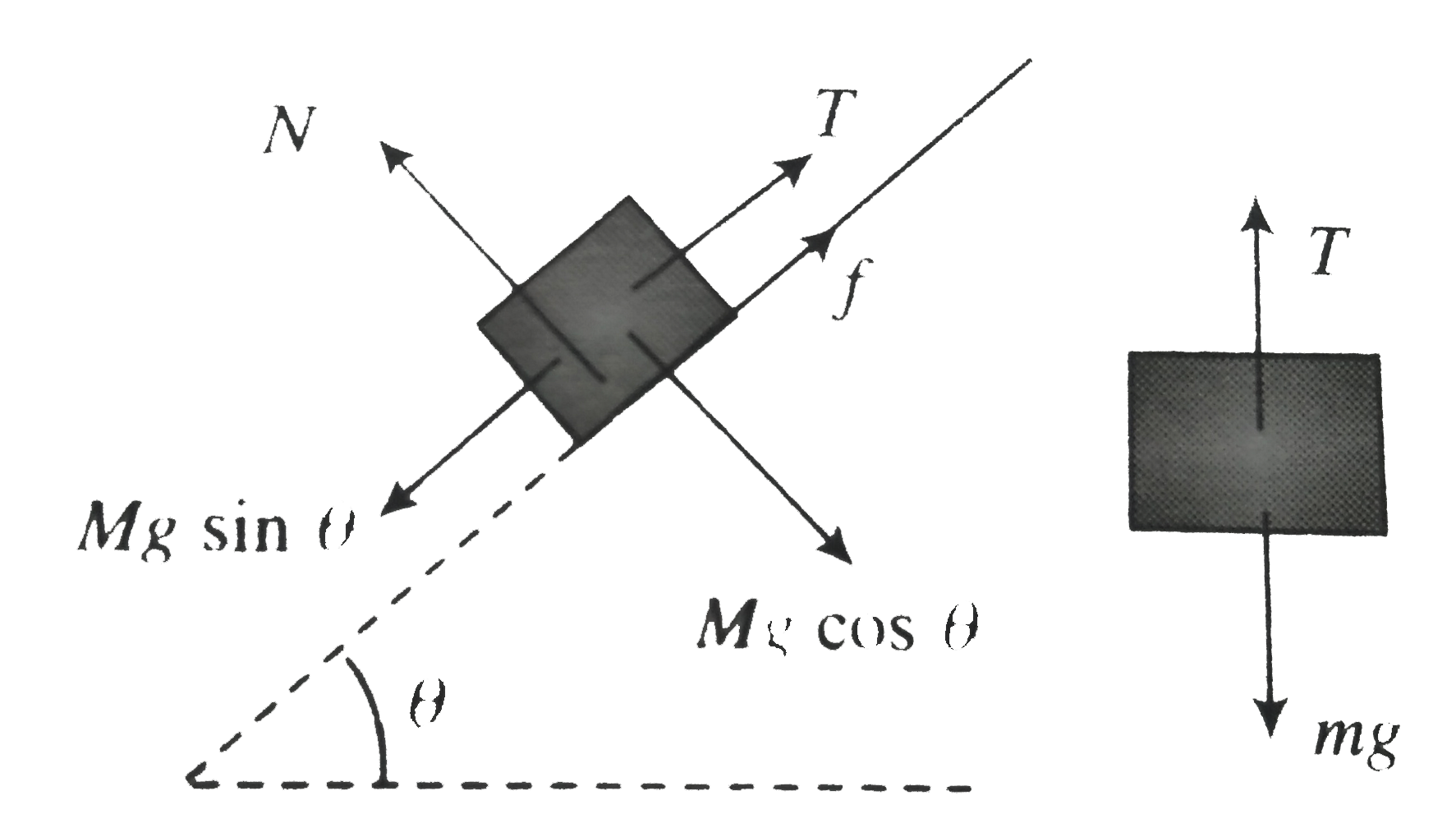
For Equation of `M:f = Mg sin theta - T` ...(i)
For Equation of `m : T = Mg `...(ii) from(i) and (ii) `f = Mg sin theta - mg` ....(iii)
for friction to be static`f lt f_(max)`
`Mg sin theta - mg + mu_(s) (Mg sin theta)`
`rArr M sin theta - mu_(s) cos theta lt m`
Hence , `mgt M(sin theta - mu_(s) cos theta) ` ...(iv)
or `m gt 50 ((3)/(5) - (3)/(5) xx (4)/(5)) rArr m gt 6`
Hence minimum value of mass `m_("min") = 6 kg`
If block `M` has the tendency in slide down the friction with act in downward direction by the relation we get the maximum value of `m` This static of as can be obtation by simply substing `(mu_(s))` is place of `mu_(s)` in fig (iv) finaly we will get the relation
`m gt M(sin theta - (- mu_(s)) cos theta)`
`rArr m gt M(sin theta + mu_(s)) cos theta)`
`m lt 50((3)/(5) + (3)/(5) xx (4)/(5)) rArr m lt 54 kg`
Hence the maximum value of mass `m_(max) = 54 kg`

