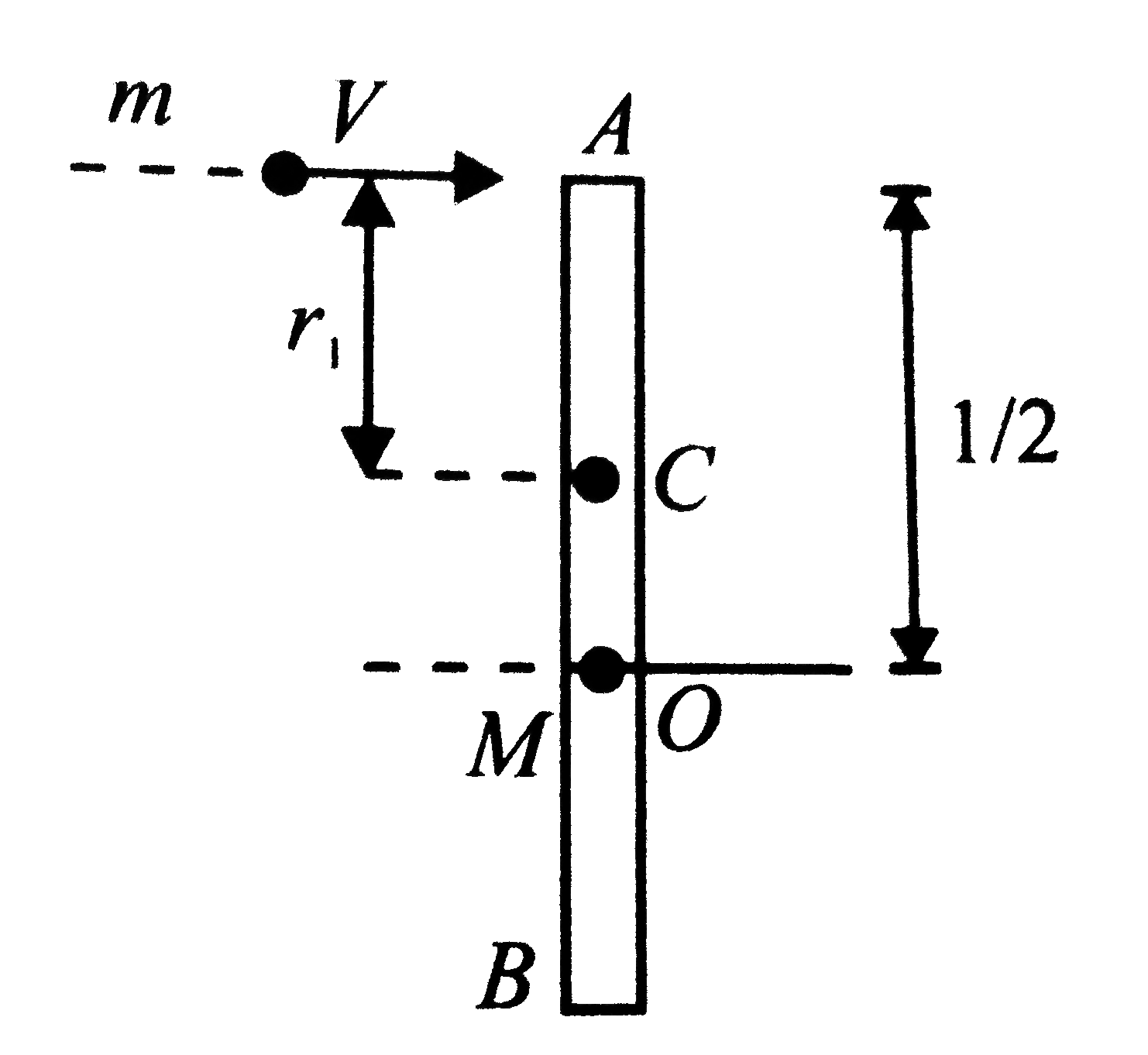
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
RIGID BODY DYNAMICS 2
CENGAGE PHYSICS|Exercise Integer|7 VideosView PlaylistRIGID BODY DYNAMICS 2
CENGAGE PHYSICS|Exercise Fill In The Blanks|7 VideosView PlaylistRIGID BODY DYNAMICS 2
CENGAGE PHYSICS|Exercise Multiple Correct|26 VideosView PlaylistRIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Integer|11 VideosView PlaylistSOUND WAVES AND DOPPLER EFFECT
CENGAGE PHYSICS|Exercise Integer|16 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-RIGID BODY DYNAMICS 2-Linked Comprehension
- A uniform rod of length L lies on a smooth horizontal table. The rod h...
01:59
|
Play - A uniform rod of length L lies on a smooth horizontal table. The rod h...
02:49
|
Play - A uniform rod of length L lies on a smooth horizontal table. The rod h...
02:49
|
Playing Now - A uniform rod of length L lies on a smooth horizontal table. The rod h...
08:26
|
Play - A uniform rod of length L lies on a smooth horizontal table. The rod h...
10:20
|
Play - A uniform solid cylinder of mass 2 kg and radius 0.2 m is released fro...
06:29
|
Play - A uniform solid cylinder of mass 2 kg and radius 0.2 m is released fro...
08:44
|
Play - A uniform solid cylinder of mass 2 kg and radius 0.2 m is released fro...
08:23
|
Play - A disc of a mass M and radius R can rotate freely in vertical plane ab...
02:28
|
Play - A disc of mass M and radius R can rotate freely in a vertical plane ab...
05:12
|
Play - A disc of mass M and radius R can rotate freely in a vertical plane ab...
13:18
|
Play - In the given figure F=10N, R=1m, mass of the body is 2kg and moment of...
02:38
|
Play - In the given figure F=10N, R=1m, mass of the body is 2kg and moment of...
04:08
|
Play - A disc of radius 20 CM is rolling with slipping on a flat horizontal s...
02:19
|
Play - A disc of radius 0.2 m is rolling with slipping on a flat horizontal s...
02:48
|
Play - A disc of radius 20 CM is rolling with slipping on a flat horizontal s...
03:10
|
Play - A solid sphere of mass M and radius R is initially at rest. Solid sphe...
06:21
|
Play - A solid sphere of mass M and radius R is initially at rest. Solid sphe...
07:42
|
Play - A uniform rod AB hinged about a fixed point P is initially vertical. A...
07:26
|
Play - A uniform rod AB hinged about a fixed point P is initially vertical. A...
07:08
|
Play