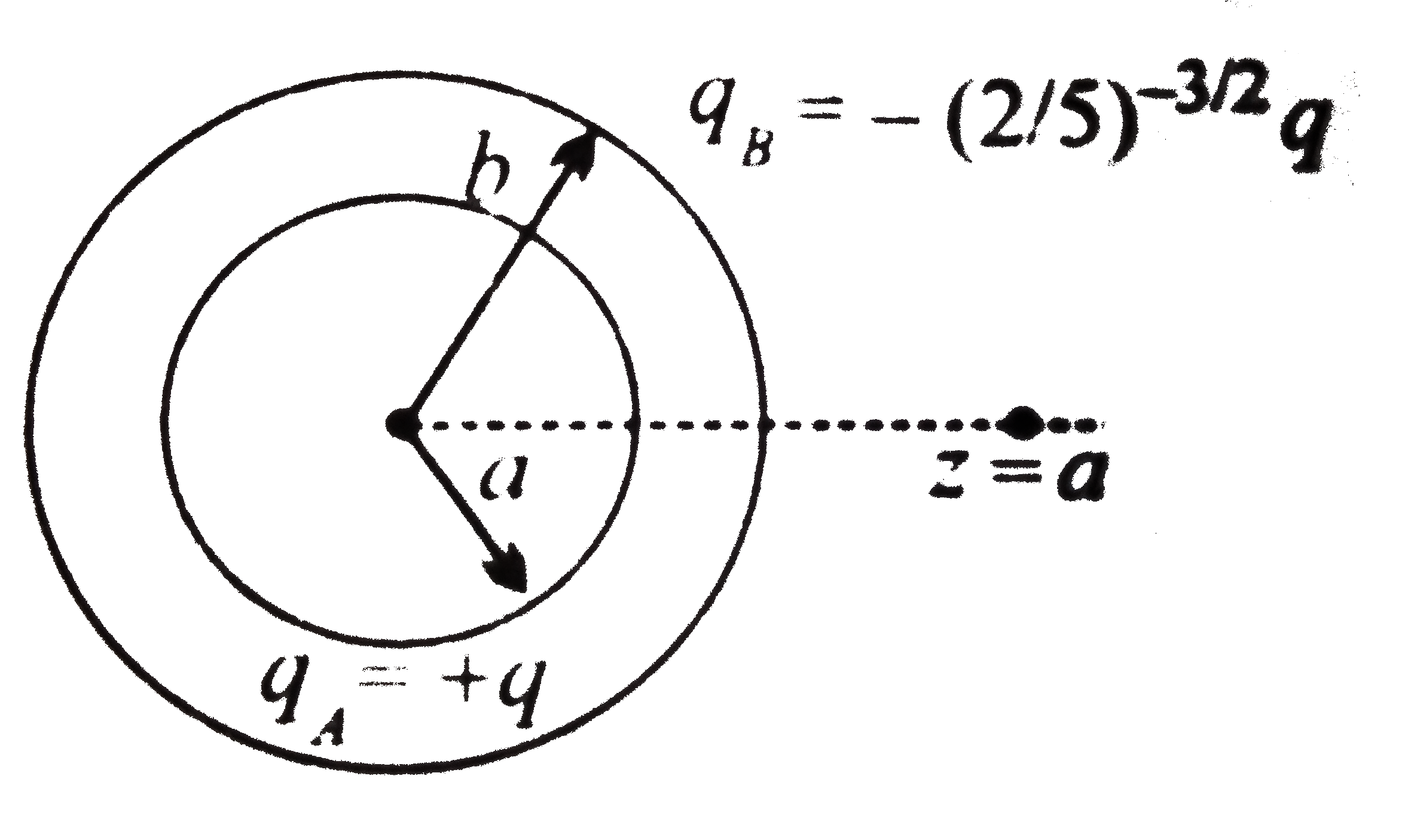Home
Class 12
PHYSICS
Two concentric rings, one of radius a an...

Two concentric rings, one of radius a and the other of radius b, have the charges +q, and `-(2//5)^(-3//2)q`, respectively as shown in fig.

Find the ratio `b//a` if a charge particle placed on the axis at z =a is in equilibrium.

Text Solution

Verified by Experts

The correct Answer is:
2
For the equilbrium of charge at z=a, the net electric field at this point due to both the rings should be zero.
`E_(A)+E_(B)=0implies(kq_(A)a)/((a^(2)+a^(2))^(3//2))+(kq_(B)a)/((b^(2)+a^(2))^(3//2))=0`
Put the value and solve to get `b//a=2`.
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • COULOMB LAW AND ELECTRIC FIELD

    CENGAGE PHYSICS|Exercise Single Correct Ansewr Type|20 Videos

  • COULOMB LAW AND ELECTRIC FIELD

    CENGAGE PHYSICS|Exercise Multiple Correct Answers Type|2 Videos

  • COULOMB LAW AND ELECTRIC FIELD

    CENGAGE PHYSICS|Exercise Comprehension|25 Videos

  • COMMUNICATION SYSTEM

    CENGAGE PHYSICS|Exercise QUESTION BANK|19 Videos

  • Current Electricity

    CENGAGE PHYSICS|Exercise QUESTION BANK|40 Videos

Similar Questions

Explore conceptually related problems

Two concentric coplanar rings one of radius a and the other of radius 2a, have charges qa and qb respectively. A charged particle is in equilibrium on their common axis at a distance a from the common centre. Then the ratio qa/qb is

Charges are placed at the corners of a square of side a as shown in the following figure. The charged particle placed at A is in equilibrium. The ratio (q_1)/(q_2) is

Knowledge Check

  • Two concentric conducting shells of radius a and (gt a) carry charges Q and -2Q respectively. The correct variation of electric intensity E as a function of r is given by

    A
    B
    C
    D

  • Two identical coaxial rings each of radius R are separated by a distance of sqrt3R . They are uniformly charged with charges +Q and -Q respectively. The minimum kinetic energy with which a charged particle (charge +q ) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is

    A
    `(Qq)/(4piepsilon_0R)`
    B
    `(Qq)/2piepsilon_0R)`
    C
    `(Qq)/(8piepsilon_0R)`
    D
    `(3Qq)/(4piepsilon_0R)`

  • Two concentric rings, one of radius R and total charge +Q and second of radius 2R and total charge -sqrt(8)Q , lie in x-y plane (i.e., z=0 plane). The common centre of rings lies at origin and the common axis coincides with z -axis. The charge is uniformly distributed on both rings. At what distance from origin is the net electric field on z -axis zero?

    A
    `(R )/(2)`
    B
    `(R )/(sqrt(2))`
    C
    `(R )/(2sqrt(2))`
    D
    `sqrt(2)R`

    • Similar Questions

    Explore conceptually related problems

    Two concentric spherical shells of radius R_(1) and R_(2) (R_(2) gt R_(1)) are having uniformly distributed charges Q_(1) and Q_(2) respectively. Find out total energy of the system.

    Four point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the resultant electric force on a charge Q

    Two positive charges q_1 and q_2 are moving with velocities v_1 and v_2 when they are at points A and B, respectively, as shown in Fig. The magnetic force experienced by charge q_1 due to the other charge q_2 is

    Charges Q, 2Q , and -Q are given to three concentric conducting sphereical shells A, B and C respectively as shown in figure. The ratio of charge on the inner and outer surface of shell C will be

    Three concentric spherical shells A, B and C having uniformly distributed total charges +Q, -2Q and +Q respectively are placed as shown. The potential at the centre will be -

    Home
    Profile