Home
Class 12
PHYSICS
We know that electric field (E ) at any ...

We know that electric field (E ) at any point in space can be calculated using the relation
`vecE = - (deltaV)/(deltax)hati - (deltaV)/(deltay)hatj - (deltaV)/(deltaz)hatk`

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as `V = 2x^2`, where x is in meter. Its variation is as shown in figure
Draw the variation of electric field (E ) along the x-axis.

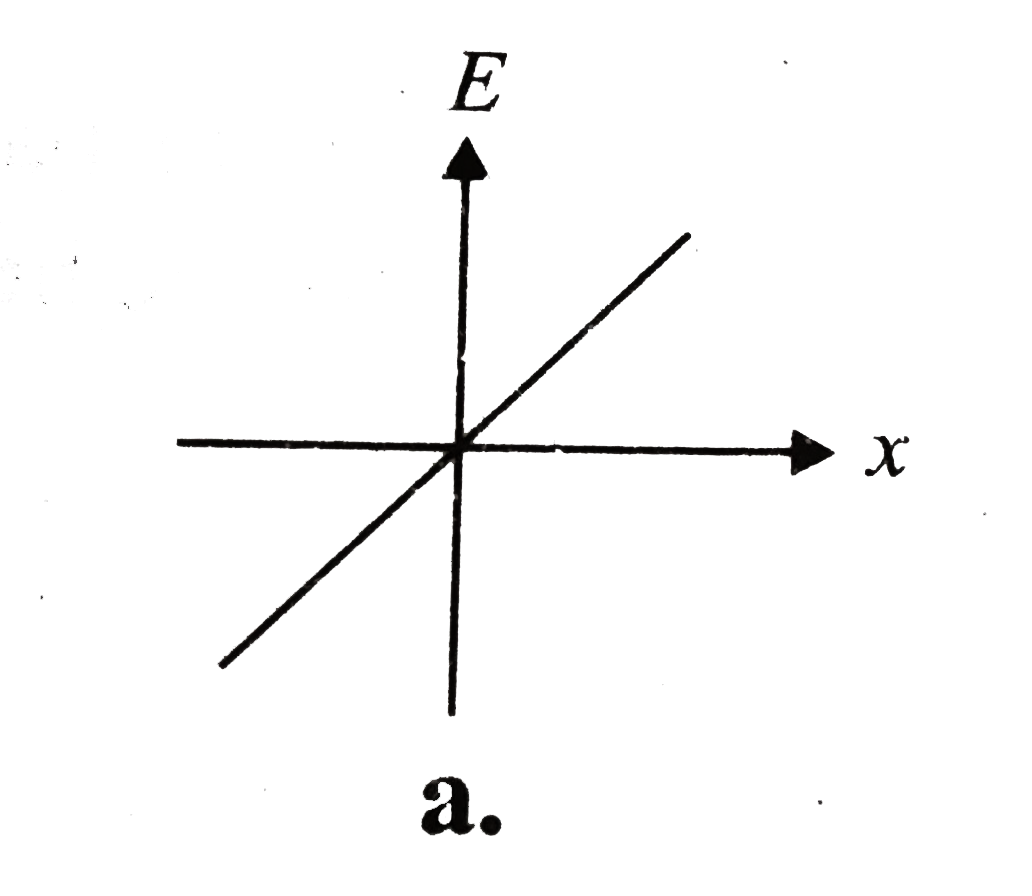
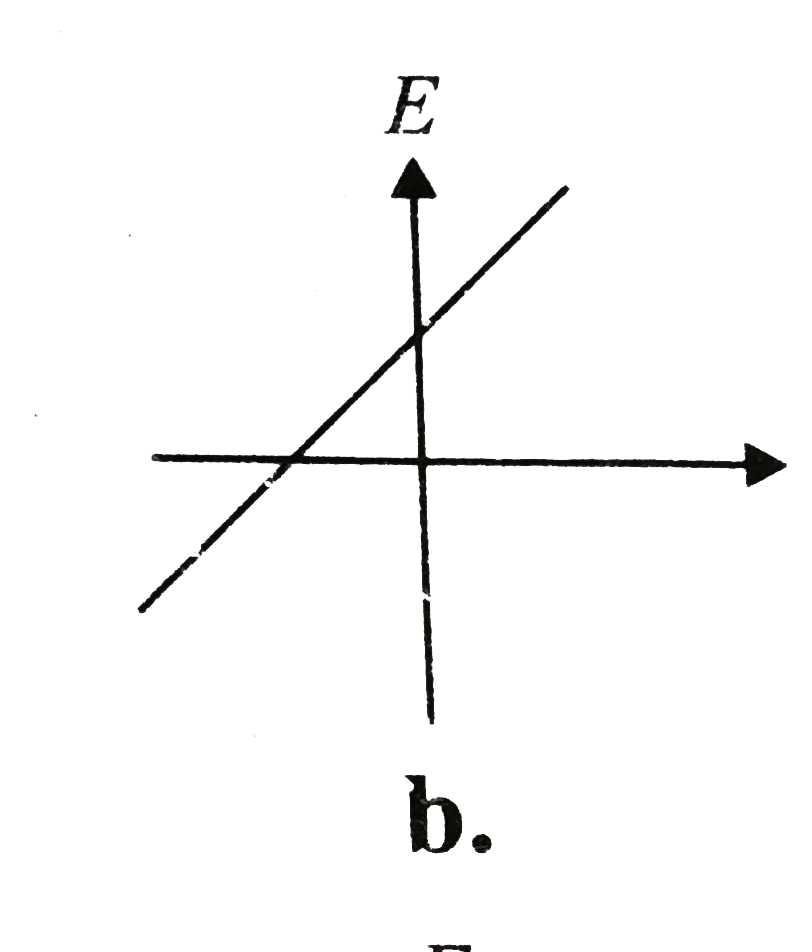
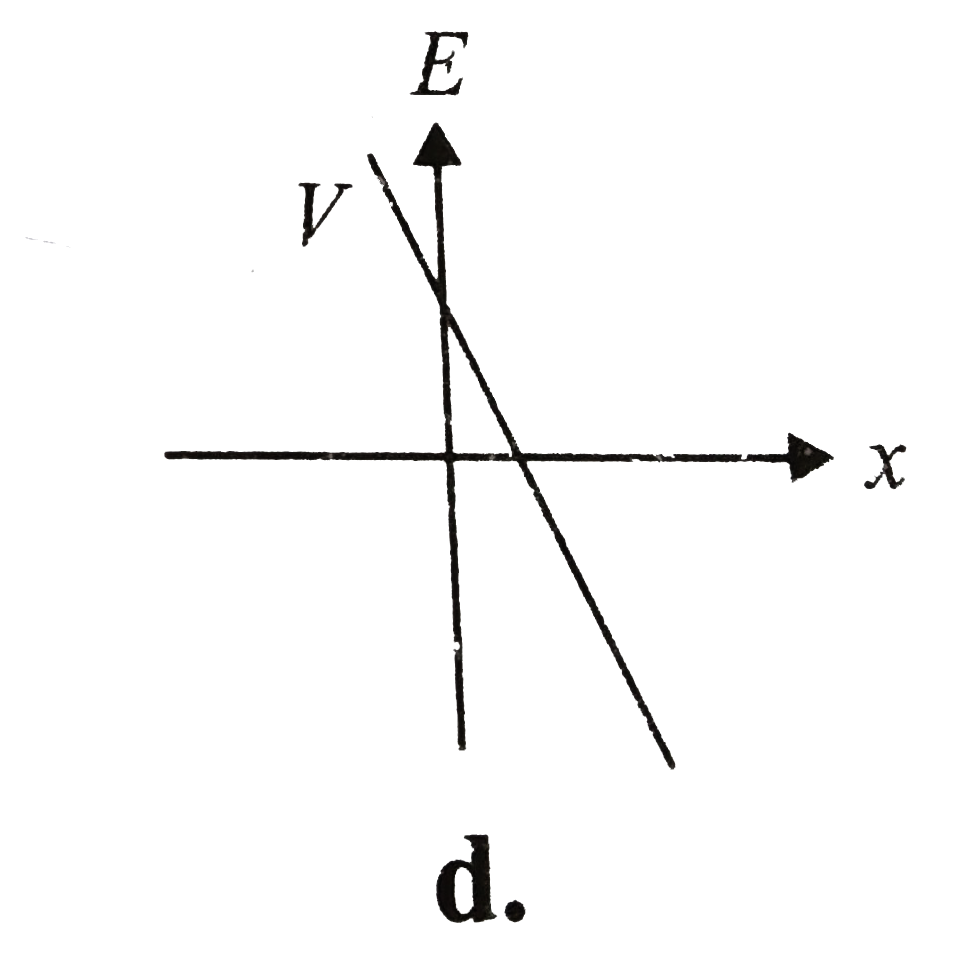
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
C
`E=-(dV)/(dx)=-4x`
`F=qE=2.5xx10^(-6)(-4x)=-10^(-5)x`
`W=underset(2)overset(0)int Fdx=-10^(-5)underset(2)overset(0)intxdx`
`(1)/(2)mv^(2)=10^(-5)[(x^(2))/(2)]_(0)^(2)` or `V=2ms^(-1)`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • MISCELLANEOUS VOLUME 3

    CENGAGE PHYSICS|Exercise Interger Answer type|20 Videos

  • MISCELLANEOUS VOLUME 3

    CENGAGE PHYSICS|Exercise Fill in the blanks|10 Videos

  • MISCELLANEOUS VOLUME 3

    CENGAGE PHYSICS|Exercise Assertion and Reason Type|8 Videos

  • MECHANICAL PROPERTIES OF SOLIDS

    CENGAGE PHYSICS|Exercise Question Bank|4 Videos

  • MISCELLANEOUS VOLUME 5

    CENGAGE PHYSICS|Exercise Integer|12 Videos

Similar Questions

Explore conceptually related problems

How can we define electric potential at any point?

The variation of electric potential for an electric field directed parallel to the x - axis is shown in (Fig. 3.110). Draw the variation of electric field strength with the x- axis. .

Knowledge Check

  • We know that electric field (E ) at any point in space can be calculated using the relation vecE = - (deltaV)/(deltax)hati - (deltaV)/(deltay)hatj - (deltaV)/(deltaz)hatk if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V = 2x^2 , where x is in meter. Its variation is as shown in figure Will the particle perform a simple harmonic motion? Also, find the time period of its oscillations.

    A
    Yes, time period `= 2pis`.
    B
    No, time period `= 2pis`
    C
    Yes, time period `= 4pis`.
    D
    The particle will perform SHM, but time period cannot be found from the given data.

  • We know that electric field (E ) at any point in space can be calculated using the relation vecE = - (deltaV)/(deltax)hati - (deltaV)/(deltay)hatj - (deltaV)/(deltaz)hatk if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V = 2x^2 , where x is in meter. Its variation is as shown in figure A charge particle of mass 10 mg and charge 2.5 muC is released from rest at x = 2 m . Find its velocity when it crosses origin.

    A
    `0.5ms^(-1)`
    B
    `1 ms^(-1)`
    C
    `2ms^(-1)`
    D
    `4 ms^(-1)`

  • In a certain region of space, variation of potential with distance from origin as we move along x-axis is given by V = 8 x^(2) + 2 , where x is the x-coordinate of a point in space. The magnitude of electric field at a point ( -4,0) is

    A
    ` - 16 V//m`
    B
    `16 V //m`
    C
    `-64 V //m`
    D
    ` 64 V //m`

    • Similar Questions

    Explore conceptually related problems

    The electric potential V at any point in space is given V = 20 x ^3 volt, where x is in meter. Calculate the electric intensity at point P (1, 0, 2).

    the electric potential in the region of space is given by : V(x)=A+Bx+Cx^(2) where V is in volts, x is in meters and A,B,C are constants.Then,

    The variation of potential with distance R from a fixed point is shown in figure. The electric field at R = 5 m is -

    Let V be the electric potential at a given point. Then the electric field E_x along x-direction at that point is given by :

    Let V be the electric potential at a given point. Then the electric field E_x along x-direction at that point is given by :

    Home
    Profile