Home
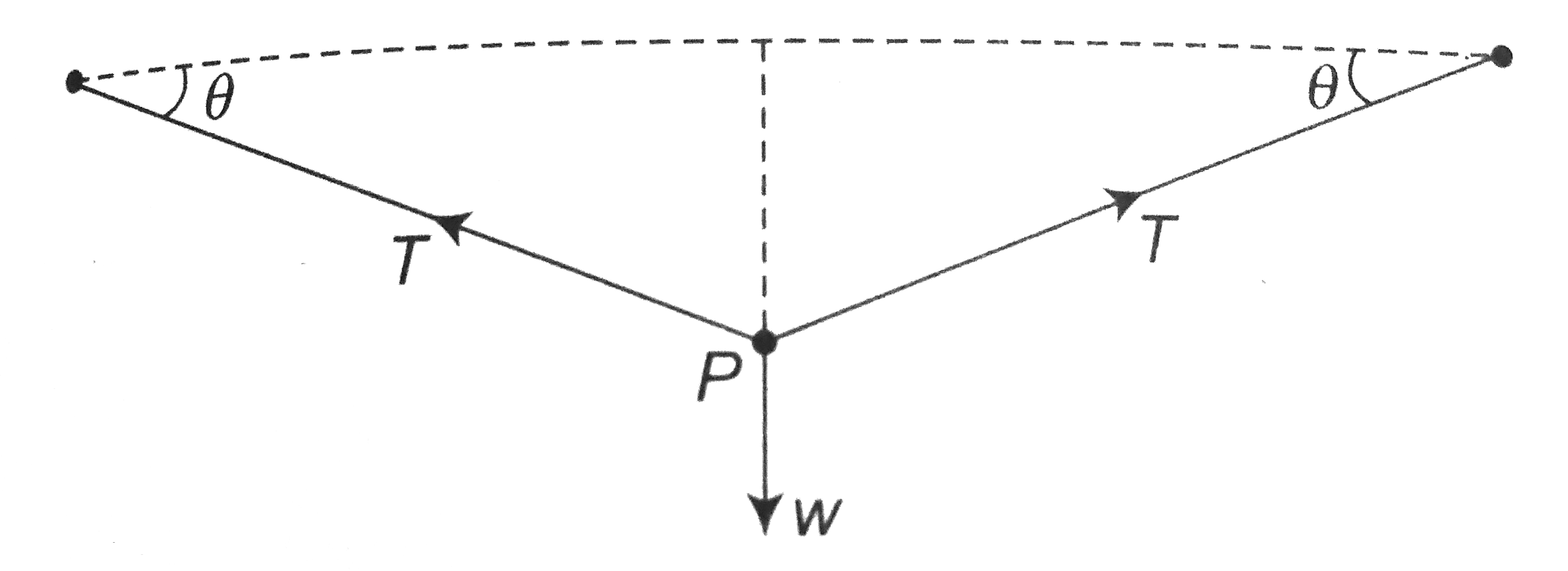
Class 11
PHYSICS
Two persons are holding a rope of neglig...

Two persons are holding a rope of negligible weight tightly at its ends so that is horizontal. A 15kg weight is attached to the mid point which how no longer remains horizontal. The minimum tension required to completely straighten the rope is:

A

15kg

B

`15//2kg`

C

5kg

D

Infinitely large

Text Solution

Verified by Experts

The correct Answer is:
D
When a string is fixed horizontal (by clamping its free ends) and loaded at the middle, then for the equilibrium of point `P`
`2Tsintheta=W` i.e., `T=(W)/(2sintheta)`
Tension in the string will be maximum when `sintheta` is minimum i.e., `theta=0^(@)` or `sintheta=0` and then `T=oo` . However, as every string can bear a maximum finite tension (lesser than breaking strenght). So this situation cannot be realized practically. We conculued that a string can never remain horizontal when loaded at the middle howsoever great the tension be applied.
Promotional Banner

Topper's Solved these Questions

  • NEWTONS LAWS OF MOTION

    A2Z|Exercise Basic Concept Of Static And Kinetic Frictions|45 Videos

  • NEWTONS LAWS OF MOTION

    A2Z|Exercise Dynamics Of Circular Motion|31 Videos

  • NEWTONS LAWS OF MOTION

    A2Z|Exercise Equilibrium Of A Particle|19 Videos

  • MOTION IN TWO DIMENSION

    A2Z|Exercise Chapter Test|29 Videos

  • OSCILLATION AND SIMPLE HARMONIC MOTION

    A2Z|Exercise Chapter Test|29 Videos

Similar Questions

Explore conceptually related problems

Two persons are holding a rope of negligible weight tightly at its ends so that it is horizontal. A 15kg weight is attached to rope at the midpoint which now no more remains horizontal The minimum tension required to completely straighten the rope is .

Two persons are holding a rope of negligible mass horizontally. A 20 kg mass is attached to the rope at the midpoint, as a result the rope deviates from the horizontal direction. The tension required to completely straighten the rope is (g=10m//s^(2))

A weight mg is suspended from the middle of a rope whose ends are at the same level. The rope is no longer horizontal. Find the minimum tenstion required to completely straighten the rope.

Two persons are pulling, the ends of a strong in such a way so that the string is stretched horizontally. When a weight of 10 kg is suspended in the middle of the string. The string does not remanin horizontal. Can the persons maken it horizontal again by pulling it with a greater force ?

Aspring of weight W and force constant k is suspended in a horizontal position by two light strings attached to its two ends. Each string makes and angle theta with the vertical .The extension of the sporing is

A spring of weight W and force constant k is suspended is a horizontal position by tw3o ligth strings attached to its two ends. Each string makes an angle theta with the vertical. The extension of the spring is.

One end of a horizontal uniform beam of weight W and length L is hinged on a vertical wall at point O and its other end is supported by a light inextensible rope. The other end of the rope is fixed at point Q at a height L above the hinge at point O. A block of weight alpha W is attached at the point Q at a height L above the hinge at point O. A block of weight alpha W is attached at the point P of the beam as shown in the figure. The rope can sustain a maximum tension of 2(sqrt(2)) W . Which of the following statements is/are correct?

The sphere at A is given a downward velocity v_(0) of magnitude 5m//s and swings in a vertical plane at the end of a rope of length l=2m attached to a support at O . Determine the angle theta at which the rope will breack, knowing that it can withstant a maximum tension equal to twich the weight of the sphere.

A uniform rod of length L and weight W is suspended horizontally by two vertical ropes as shown. The first rope is attached to the left end of the rod while the second is attached to the left end of the rod while the second rope is attached a distance L//4 from the right end. The tension in the second rope is. .

Knowledge Check

  • Two persons are holding a rope of negligible weight tightly at its ends so that it is horizontal. A 15kg weight is attached to rope at the midpoint which now no more remains horizontal The minimum tension required to completely straighten the rope is .

    A
    `150N`
    B
    `75N`
    C
    `50N`
    D
    Infinitely large

  • Two persons are holding a rope of negligible weight tightly at its ends so that it is horizontal. A 15 kg weight is attached to rope at the midpoint which now no more remains horizontal. The minimum tension required to completely straighten the rope is

    A
    150 N
    B
    75 N
    C
    50 N
    D
    Infinitely large

  • Aspring of weight W and force constant k is suspended in a horizontal position by two light strings attached to its two ends. Each string makes and angle theta with the vertical .The extension of the sporing is

    A
    `(W//4k)tantheta`
    B
    `(W//2k)tantheta`
    C
    `(W//4k)sintheta`
    D
    0
    • A2Z-NEWTONS LAWS OF MOTION-Applications Of Newton'S Laws Of Motion
    1. Two persons are holding a rope of negligible weight tightly at its end...

      Text Solution

      |

    2. M is a fixed wedge. Masses m(1) and m(2) are connected by a light stri...

      Text Solution

      |

    3. With what acceleration 'a' should the box of figure moving up so that ...

      Text Solution

      |

    4. The elevator shown in fig. is descending with an acceleration of 2ms^(...

      Text Solution

      |

    5. An elevator is accelerating upwards with an acceleration of 6m//s^(2) ...

      Text Solution

      |

    6. In the given diagram, with what force must the man pull the rope to ho...

      Text Solution

      |

    7. Consider the three cases given in figures shown. Assume the friction t...

      Text Solution

      |

    8. Consider the system as shown in the figure. The pulley and the string ...

      Text Solution

      |

    9. A boy and a block, both of same mass, are suspended at the same horizo...

      Text Solution

      |

    10. In order to raise a mass of 100kg a of mass 60kg fastens a rope to it ...

      Text Solution

      |

    11. Two masses of 1kg and 5kg are attached to the ends of a massless strin...

      Text Solution

      |

    12. Three equal weight A,B and C of mass 2kg each are hanging on a string ...

      Text Solution

      |

    13. Two bodies of mass 4kg and 6kg are attached to the ends of a string pa...

      Text Solution

      |

    14. Figure shown two pulley arrangements for lifting a mass m . In case-1,...

      Text Solution

      |

    15. In fig the blocks A, B, and C of mass m each have acceleration a(1),a(...

      Text Solution

      |

    16. Two block are connected by a string as shown in the diagram. The upper...

      Text Solution

      |

    17. Three blocks are connected as shown in figure on a horizontal friction...

      Text Solution

      |

    18. A force F is applied on block A as shown in the figure. The contact fo...

      Text Solution

      |

    19. Two small sphere each of mass m connected by a string of length 2l are...

      Text Solution

      |

    20. A perfectly straight portion of a uniform rope has mass M and length L...

      Text Solution

      |