A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
ROTATIONAL DYNAMICS
A2Z|Exercise Displacement , Velocity And Acceleration Of Centre Of Mass|30 VideosView PlaylistROTATIONAL DYNAMICS
A2Z|Exercise Moment Of Inertia|39 VideosView PlaylistPROPERTIES OF MATTER
A2Z|Exercise Chapter Test|29 VideosView PlaylistTHERMAL PROPERTIES OF MATTER
A2Z|Exercise Chapter Test|30 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
A2Z-ROTATIONAL DYNAMICS-Chapter Test
- A square of side a and uniform thickness is divided into four equal pa...
04:26
|
Playing Now - A carpenter has constructed a toy as shown in figure. If the density o...
03:08
|
Play - From a given sample of uniform wire, two circular loops P and Q are ma...
02:45
|
Play - A particle of mass m is moving in a plane along a circular path of rad...
01:19
|
Play - A particle performing uniform circular motion gas angular momentum L. ...
01:36
|
Play - A solid sphere rolls down two different inclined planes of the same he...
07:46
|
Play - What is the minimum value of coefficient of friction between the cylin...
06:37
|
Play - The kinetic energy of an object rotating about a fixed axis with angul...
01:08
|
Play - An ice skater starts a spin with her arms stretched out to the sides. ...
01:34
|
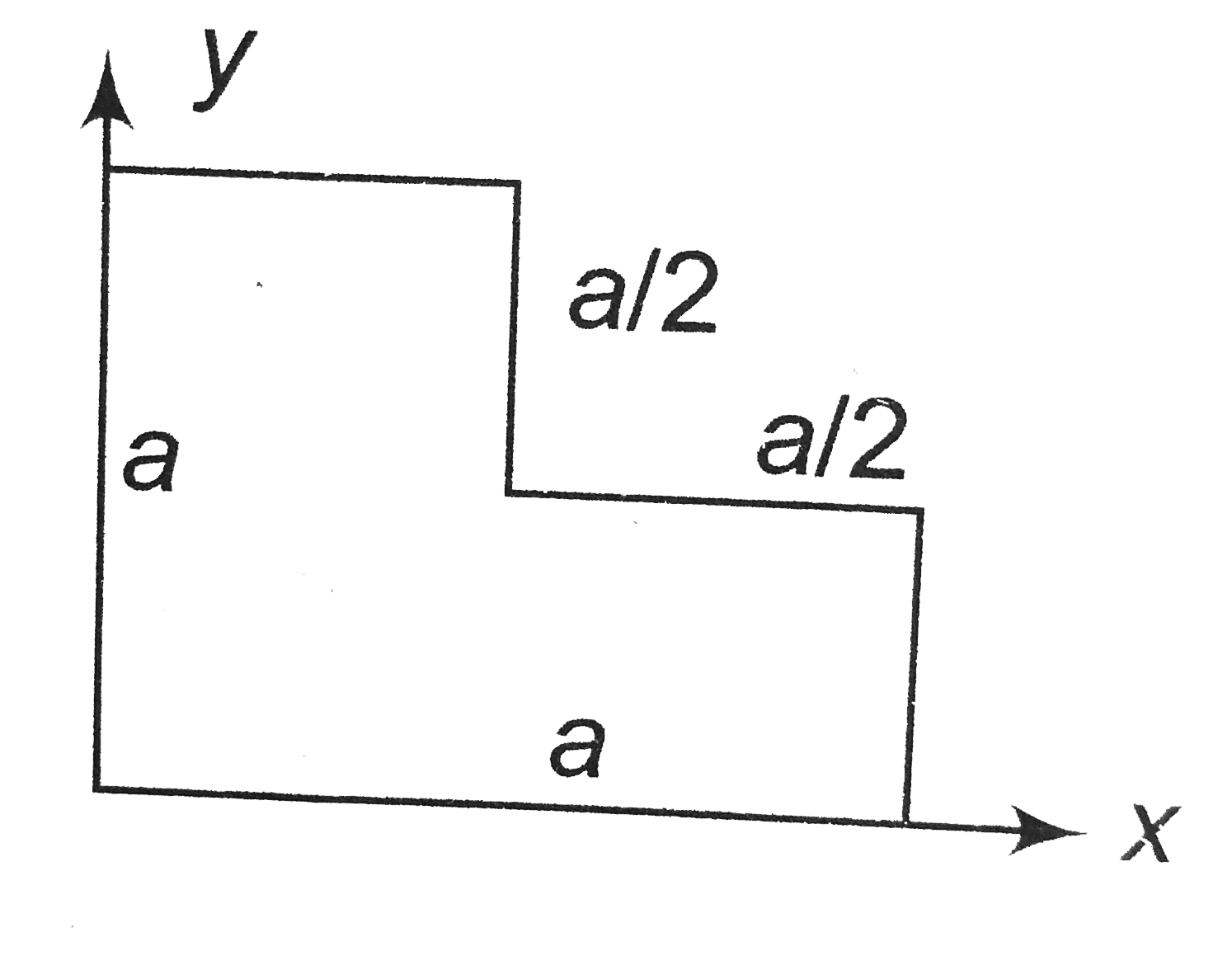
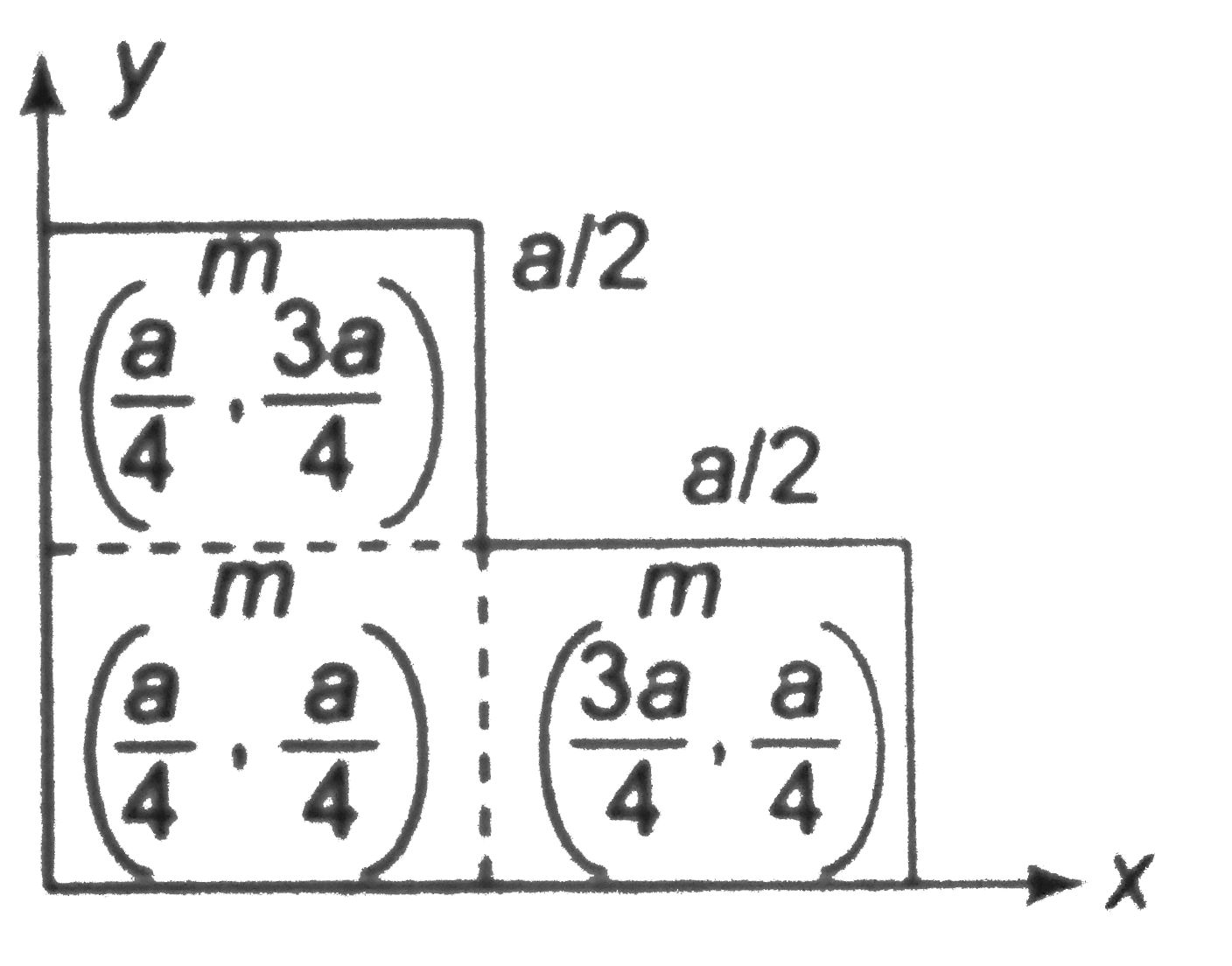
Play - Find the centre of mass of a uniform L shaped lamina (a thin flat plat...
04:07
|
Play - From a uniform disc of radius R, a circular section of radius R//2 is ...
05:21
|
Play - Half of the recrtangular plate shown in figure is made of a material o...
07:26
|
Play - With reference to Fig. of a cube of edge a and mass m, state whether t...
03:35
|
Play - The moment of inertia of a uniform thin rod of mass m and length l abo...
01:45
|
Play - Wheels A and B in Figure are connected by a belt that does not slip. T...
02:20
|
Play - A disc of radius R and mass M is rolling horizontally without slipping...
01:52
|
Play - A sphere of outer radius R having some cavity inside is allowed to rol...
02:47
|
Play - In a bicycle the radius of rear wheel is twice the radius of front whe...
01:55
|
Play - A cord is wound round the circumference of wheel of radius r. The axis...
03:35
|
Play - Two identical cylinders roll from rest on two identical planes of slan...
01:42
|
Play - A solid cylinder and a hollow cylinder, both of the same mass and same...
05:05
|
Play
 .
. .
.