Text Solution
Verified by Experts
Topper's Solved these Questions
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
PRADEEP|Exercise QUESTIONS|15 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
PRADEEP|Exercise VALUE BASED QUESTIONS|5 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
PRADEEP|Exercise NCERT|21 VideosRAY OPTICS
PRADEEP|Exercise Problem For Practice(a)|25 VideosTHERMODYNAMICS
PRADEEP|Exercise Assertion- Reason Type Questions|19 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-ADDITIONAL EXERCISES
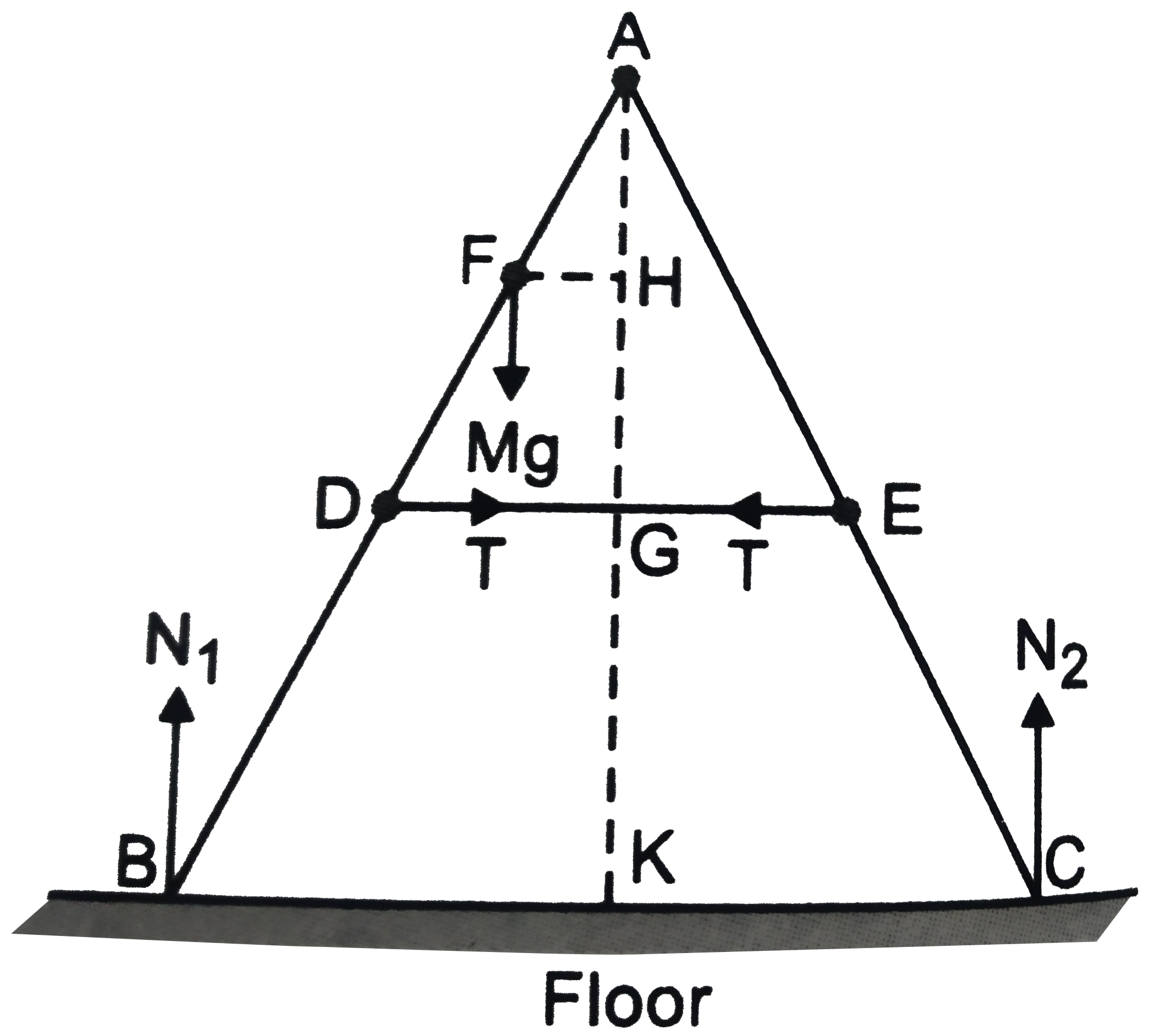
- As shown in Fig. the two sides of a step ladder BA and CA are 1.6 m lo...
Text Solution
|
- A man stands on a rotating platform, with his arms stretched horizonta...
Text Solution
|
- A bullet of mass 10 g and speed 500 m//s is fired into a door and gets...
Text Solution
|
- Two discs of moments of inertia I(1) and I(2) about their respective a...
Text Solution
|
- (a) Prove the theorem of perpendicular axes. (Hint : Square of the d...
Text Solution
|
- Prove the result that the velocity v of translation of a rolling body ...
Text Solution
|
- A disc roating about its axis with angular speed omega(0) is placed li...
Text Solution
|
- (i) Explain why friction is necessary to make the disc to roll in the ...
Text Solution
|
- A solid disc and a ring, both of radius 10 cm are placed on a horizont...
Text Solution
|
- A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a pl...
Text Solution
|
- Read each statement below carefully and state with reasons, if it is t...
Text Solution
|