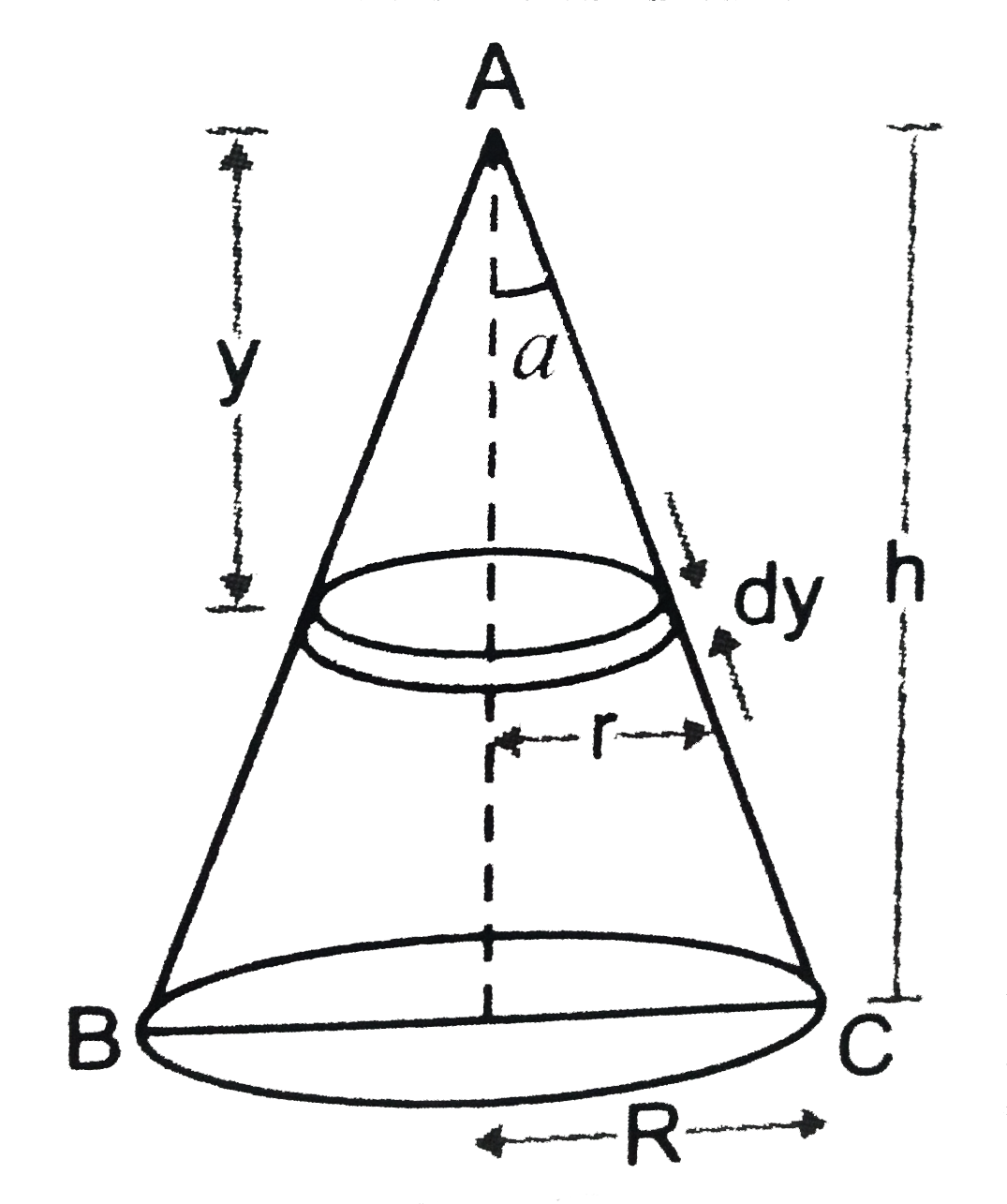
Distance of the centre of mass of a soli...

Distance of the centre of mass of a solid uniform cone from its vertex is `z_0`. If the radius of its base is R and its height is h then `z_0` is equal to:

`(h^(2))/(4R)`

`(3h)/(4)`

`(5h)/(8)`

`(3h^(2))/(8R)`

Text Solution

Verified by Experts

The correct Answer is:

Let distnace of c.m from the vertex, `Z_(0) = y_(cm)`

Let density of cone `= rho`
`Z_(0) = y_(cm) = (int y dm)/(int dm)`
`= (int_(0)^(h) y pi r^(2)dy rho)/((1)/(3)piR^(2)h rho) = (int_(0)^(h) r^(2)ydy) /((1)/(3)R^(2)h)` ..(i)
As `(r )/(R ) = (y)/(h), :. r = (y)/(h)R`, putting value of y in (i)
`Z_(0) = y_(cm) =(int_(0)^(h)3 y^(3) dy)/(h^(3)) =(3[(y^(4))/(4)]_(0)^(h))/h^(3) = (3)/(4)h`

Topper's Solved these Questions

SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
PRADEEP|Exercise Multiple Choice Questions II.|1 Videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
PRADEEP|Exercise Multiple Choice Questions III. Comprehension 1|1 Videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
PRADEEP|Exercise MULTIPLE CHOICE QUESTIONS-II|1 Videos
RAY OPTICS
PRADEEP|Exercise Problem For Practice(a)|25 Videos
THERMODYNAMICS
PRADEEP|Exercise Assertion- Reason Type Questions|19 Videos

Distance of the centre of mass of a solid uniform cone from it's vertex is Zo. If the radius of it's base is R and it's height is h, the Zo is equal to

`b^(2)/(4R)`

`(3b)/(4)`

`(5h)/8`

`(3h^(2))/(8R)`

The centre of mass of a solid cone along the line form the center of the base to the vertex is at

One-fourth of the height

One-third of the height

One-fifth of the height

None of these

The distance of the centre of mass of a hemispherical shell of radius R from its centre is

`R/2`

`R/3`

`(2R)/2`

`(2R)/3`