Text Solution
Verified by Experts
Topper's Solved these Questions
CIRCLE
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise PRACTICE SET 3.5|6 VideosCIRCLE
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise PROBLEM SET 3|50 VideosCIRCLE
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise PRACTICE SET 3.3|3 VideosCHALLENGING QUESTIONS
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :|1 VideosCOORDINATE GEOMETRY
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Assignment 6.5|13 Videos
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-CIRCLE-PRACTICE SET 3.4
- In the figure, in a circle with centre O, length of chord AB is equal...
Text Solution
|
- In the figure , in a circle with centre O, length of chord AB is equal...
Text Solution
|
- In the figure , in a circle with centre O, length of chord AB is equal...
Text Solution
|
- In the figure , in a circle with centre O, length of chord AB is equal...
Text Solution
|
- In the figure, square PQRS is cyclic side PQ cong RQ, /PSR=110^(@), Fi...
Text Solution
|
- In the figure, square PQRS is cyclic side PQ cong RQ, /PSR=110^(@), Fi...
Text Solution
|
- In the figure, square PQRS is cyclic side PQ cong RQ, /PSR=110^(@), Fi...
Text Solution
|
- In the figure, square PQRS is cyclic side PQ cong RQ, /PSR=110^(@), Fi...
Text Solution
|
- square MRPN is cyclic , / R = ( 5x - 13) ^(@) , / N = ( 4x + 4)^(@) .F...
Text Solution
|
- In figure, seg RS is a diameter of the circle with centre O. Point T l...
Text Solution
|
- Prove that, any rectangle is a cyclic quadrilateral.
Text Solution
|
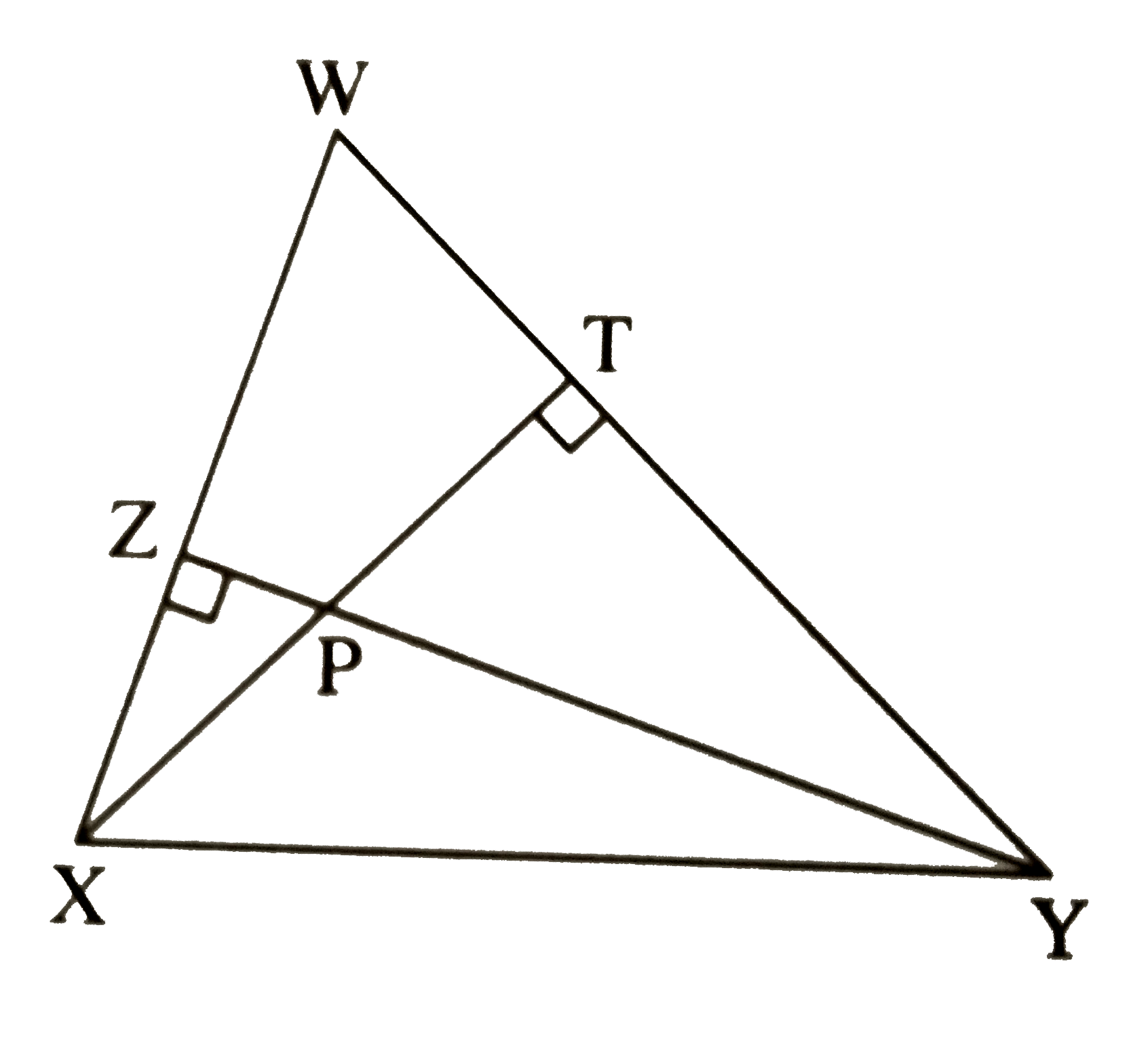
- In figure, altitudes YZ and XT of triangle WXY intersect at P. Prove ...
Text Solution
|
- In figure, altitudes YZ and XT of triangle WXY intersect at P. Prove ...
Text Solution
|
- In the figure, m ) arc NS ) = 125^(@) m ( arc EF ) = 37^(@) find...
Text Solution
|
- In the figure, chords AC and DE intersect at B. If /ABE = 108^(@), m (...
Text Solution
|