A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
DUAL NATURE OF RADIATION AND MATTER
A2Z|Exercise Photo Momentum Energy|30 VideosView PlaylistDUAL NATURE OF RADIATION AND MATTER
A2Z|Exercise Photo Electric Effect|61 VideosView PlaylistCURRENT ELECTRICITY
A2Z|Exercise Section D - Chapter End Test|29 VideosView PlaylistELECTRIC CHARGE, FIELD & FLUX
A2Z|Exercise Section D - Chapter End Test|29 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
A2Z-DUAL NATURE OF RADIATION AND MATTER-Section D - Chapter End Test
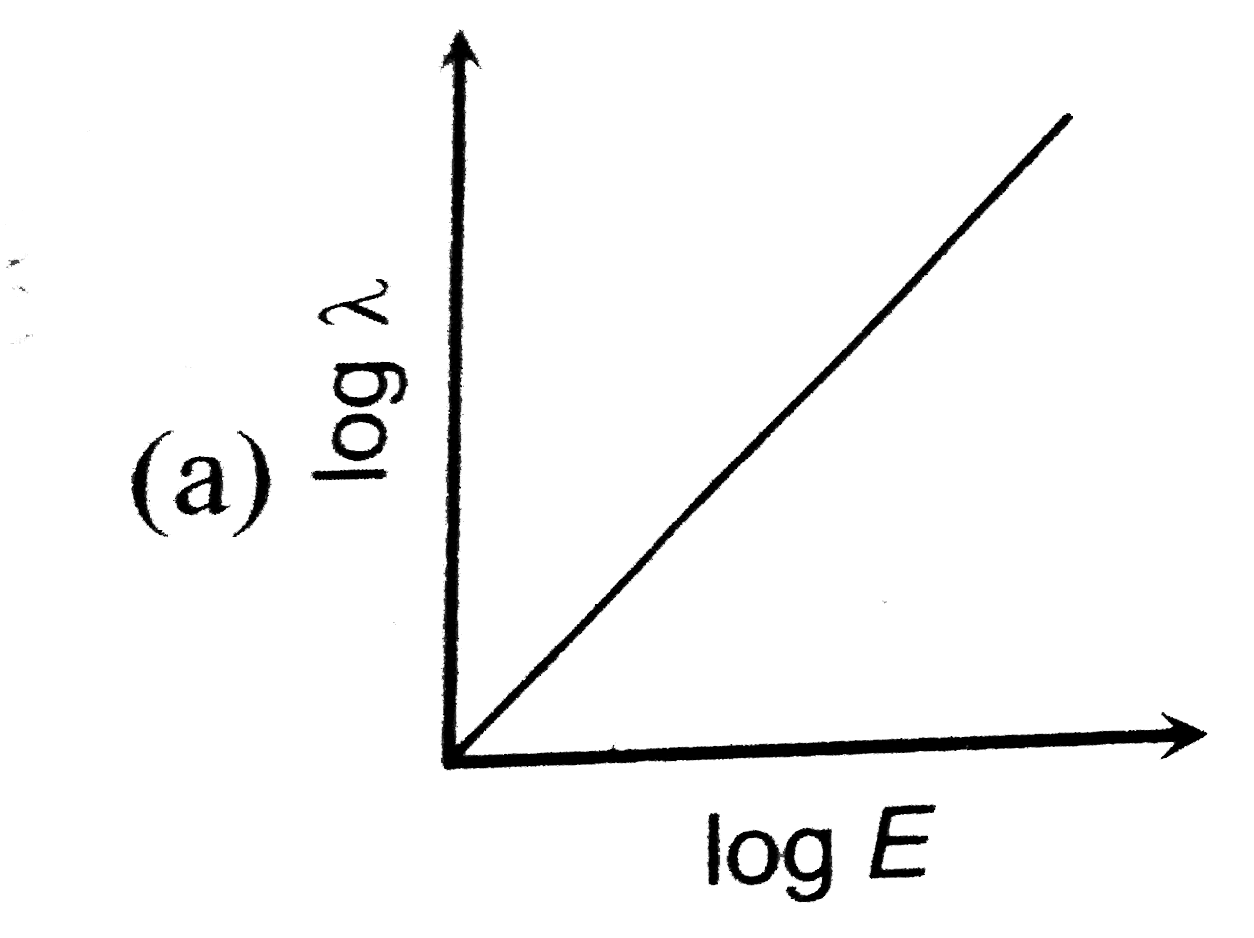
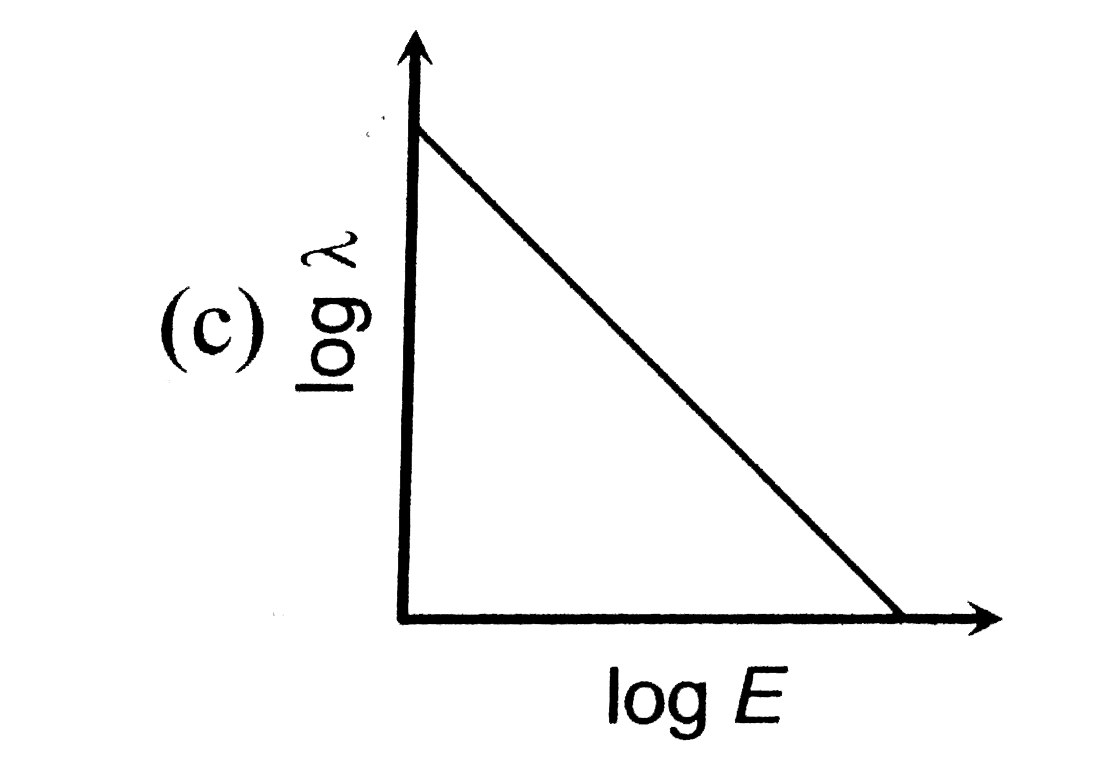
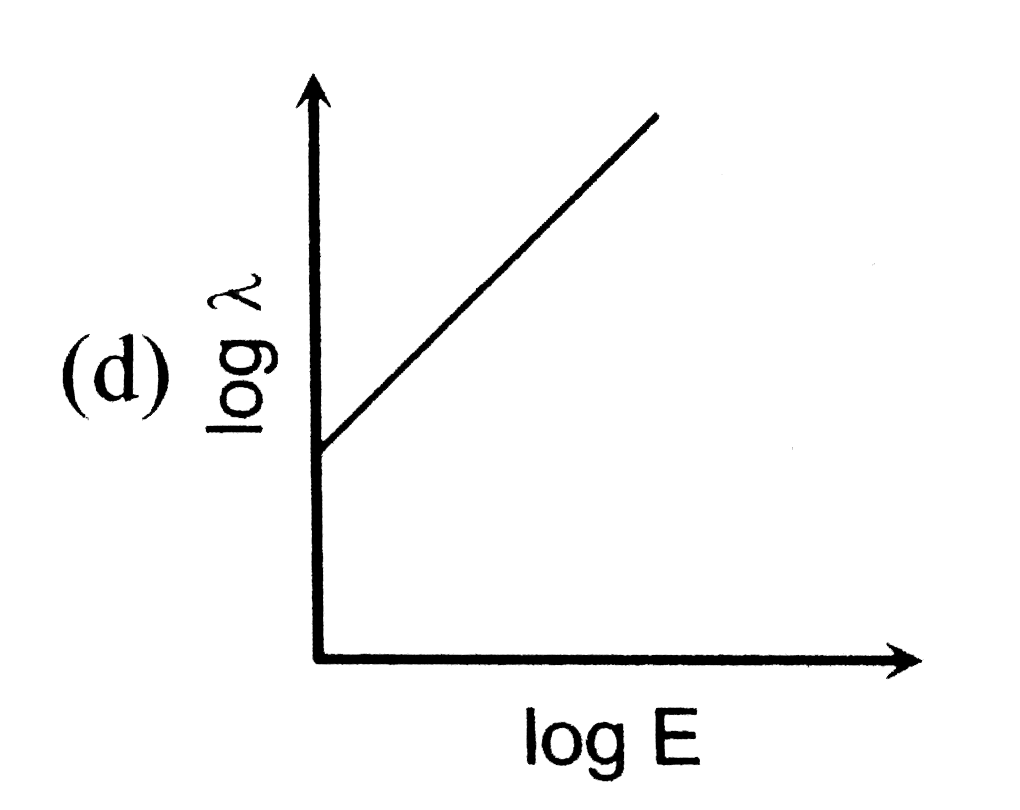
- The log - log graph between the energy E of an electron and its de - B...
03:03
|
Playing Now - If a photon has velocity c and frequency n , then which of following r...
00:54
|
Play - Lights of two different frequencies whose photons have energies 1 and ...
01:38
|
Play - Sodium and copper have work functions 2.3 eV and 4.5 eV respectively ....
02:44
|
Play - Two identical photocathodes receive light of frequency f(1) andf(2) if...
01:46
|
Play - The work function of a substance is 4.0 eV. The longest wavelength of ...
03:40
|
Play - According to Einstein's photoelectric equation, the plot of the maximu...
00:53
|
Play - A photocell is illuminated by a small bright source places 1 m away w...
01:36
|
Play - If the kinetic energy of a free electron doubles , its de - Broglie wa...
02:02
|
Play - In a photoelectric effect , the K.E. of electrons emitted from the met...
03:03
|
Play - The photoelectric effect can be understood on the basis of
02:20
|
Play - If the threshold wavelength for sodium is 5420 Å, then the work functi...
02:42
|
Play - The magnitude of saturation photoelectric current depends upon
03:59
|
Play - For photoelectric emission , tungsten requires light of 2300 Å. If lig...
01:20
|
Play - The light rays having photons of energy 1.8 eV are falling on a metal ...
02:07
|
Play - A photon of energy 8 eV is incident on metal surface of threshold fre...
01:41
|
Play - In the diagram a graph between the intensity of X-rays emitted by a mo...
03:16
|
Play - The maximum value of stopping potential in the following diagram is
02:37
|
Play - The variation of wavelength lambda of the K(alpha) line with atomic nu...
02:09
|
Play - From the figure describing photoelectric effect we may infer correctly...
06:45
|
Play - When an inert gas is filled in the place vacuum in a photo cell , then
03:42
|
Play