(i) Draw the plot of amplitude versus `omega` for an amplitude modulated were whose carrier wave `(omega_(c))` is carrying two modulating signals, `omega_(1)` and `omega_(2)` `(omega_(2) gt omega_(1))`.
(ii) Is the plot symmetrical about `omega_(c)` ? Comment especially about plot in region `omega lt omega_(c)`.
(iii) Extrapolate and predict the problems one can expect if more waves are to be modulated.
(iv) Suggest solutions to the above problem. In the process can one understand another advantage of modulation in terms of bandwidth?

Explanation

(i) Let the two modulating signals `A_(m_1) sin omega_(m_1)t` and `A_(m_2) sinomega_(m_2)t` be superimposed on carrier signal
`A_c sim omega_c t`. The signal produced is `x(t) = A_(m_1)sin omega_(m_1) t + A_(m_2)sin omega_(m_2) t + A_c sin omega_c t`
To produce amplitude modulated wave the signal `x (t)` is passed through a square law device which produces
an output given by
`y (t) = B[A_(m_1) sin omega_(m_1) + A_(m_2) sinomega_(m_2) t + A_(c) sinomega_(c)t ] + C [ A_(m_1) sinomega_(m_1) t + A_(m_2) sinomega_(m_2 )t + A_c sim omega_c t]^2`
`B = [A_(m_1) sinomega_(m_1) t + A_(m_2) sinomega_(m_2) t + A_(c) sinomega_(c) t] + C [(A_(m_1) sinomega_(m_1) t + A_(m_2) sinomega_(m_2)t)^2 + A_(c)^(2)sin^2omega_ct`
`+ 2A_c sin omega_ct (A_(m_1) sinomega_(m_1) t + A_(m_2) sinomega_(m_2)t)]`
`= B [ A_(m_1) sinomega_(m_1) t + A_(m_2) sinomega_(m_2)t + A_c sin omega_ct]`
`+ C [A_(m_1)^(2) sin^2 omega_(m_1) t + A_(m_2)^(2) sin^2 omega_(m_2)t + 2A_(m_1) A_(m_2) sin omega_(m_1) t sin omega_(m_2)t`
`+A_(c)^(2) sim^2 omega_ct + 2A_c (A_(m_1) sinomega_(m_1) t sin omega_c t + A_(m_2) sinomega_(m_2)t sin omega_c t)]`
`= B [ A_(m_1) sinomega_(m_1) t + A_(m_2) sinomega_(m_2)t + A_c sin omega_c t]`
`+ C [ A_(m_1)^(2) sin^2 omega_(m_1) t + A_(m_2)^(2) sin^(2) omega_(m_2)t + A_(m_1) A_(m_2) { cos (omega_(m_2) - omega_(m_1)) t - cos (omega_(m_2) + omega_(m_1))} + A_c^(2) sin^(2) omega_ct`
`+ A_c A_(m_1) {cos(omega_c - omega_(m_1)) t - cos (omega_c + omega_(m_1)) t } + A_c A_(m_2) { cos (omega_c - omega_(m_2)) t - cos (omega_c + omega_(m_2))t}]`
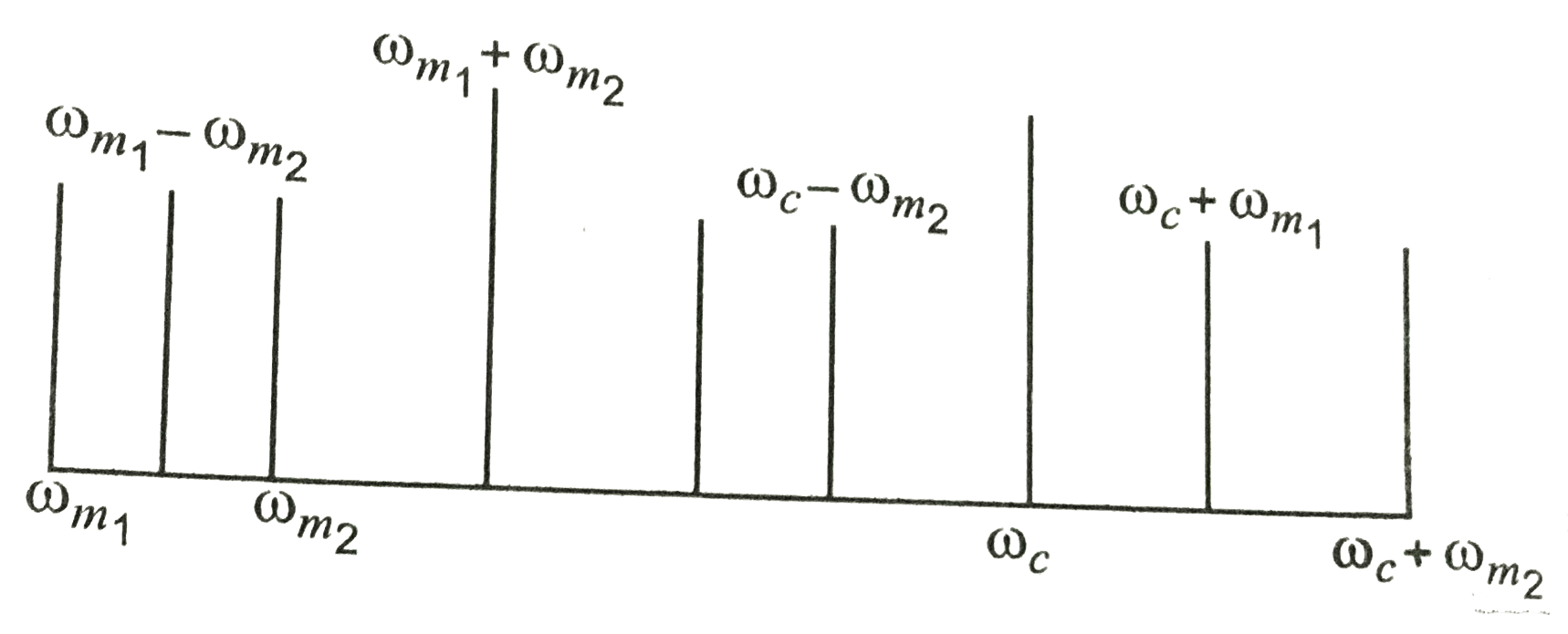
In the above amplitude modulated waves, the frequencies present are
`omega_(m_1) , omega_(m_2) , omega_c , (omega_(m_2) - omega_(m_1)), (omega_(m_2) + omega_(m_1)) , (omega_c - omega_(m_1)), (omega_c + omega_(m_1)), (omega_c - omega_(m_2))` and `(omega_c + omega_(m_2))`
The plot of amplitude versus `omega` is shown in
figure
(ii) From figure , we note that frequency
spectrum is not symmetrical about `omega_c`.
Crowding of spectrum is present for `omega lt omega_c`.
(iii) if more waves are to be modulated then
there will be more crowding in the modulating
signal in the region `omega lt omega_c`. That will result
more chances of mixing of signals.
(iv) To accommodate more signals, we should increase band width and frequency of carrier waves `omega_c`. This
shows that large carrier frequency enables to carry more information (i.e., more `omega_m`) and the same will
inturn increase band width.