Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
TARGET PUBLICATION-BOARD QUESTION PAPER: MARCH 2019-(Solve the following questions (Any one):
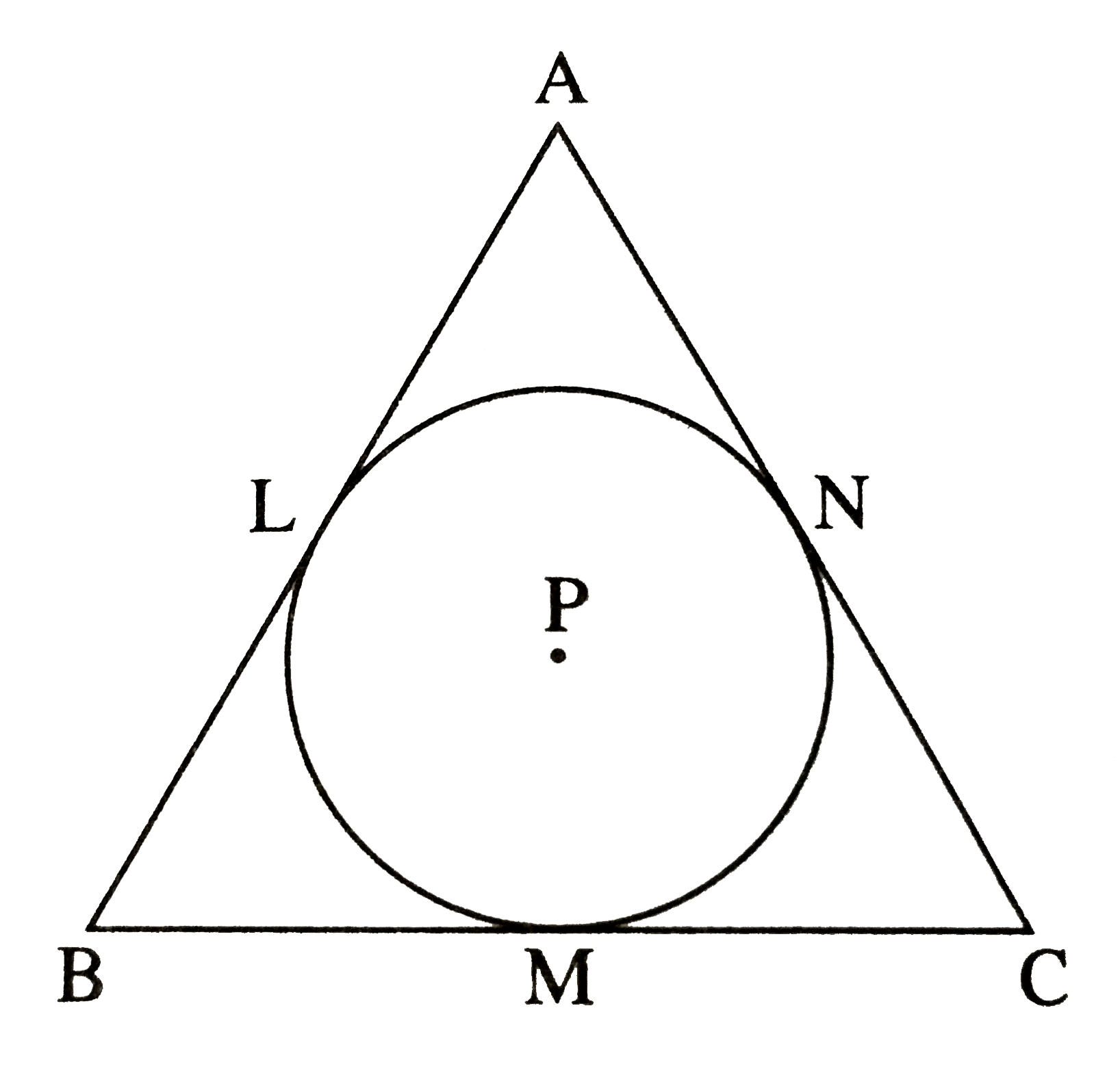
- A circle with centre P is inscribed in the triangle ABC. Side AB, side...
Text Solution
|
- In Delta ABC, angle ACB = 90^(@) ," seg "CD bot side AB and seg CE...
Text Solution
|
- Show that the points (2,0), (-2,0) and (0,2) are the vertices of a ...
Text Solution
|
- In the figure, square XLMT is a rectangle. angle M=21 cm, XL = 10. 5 c...
Text Solution
|