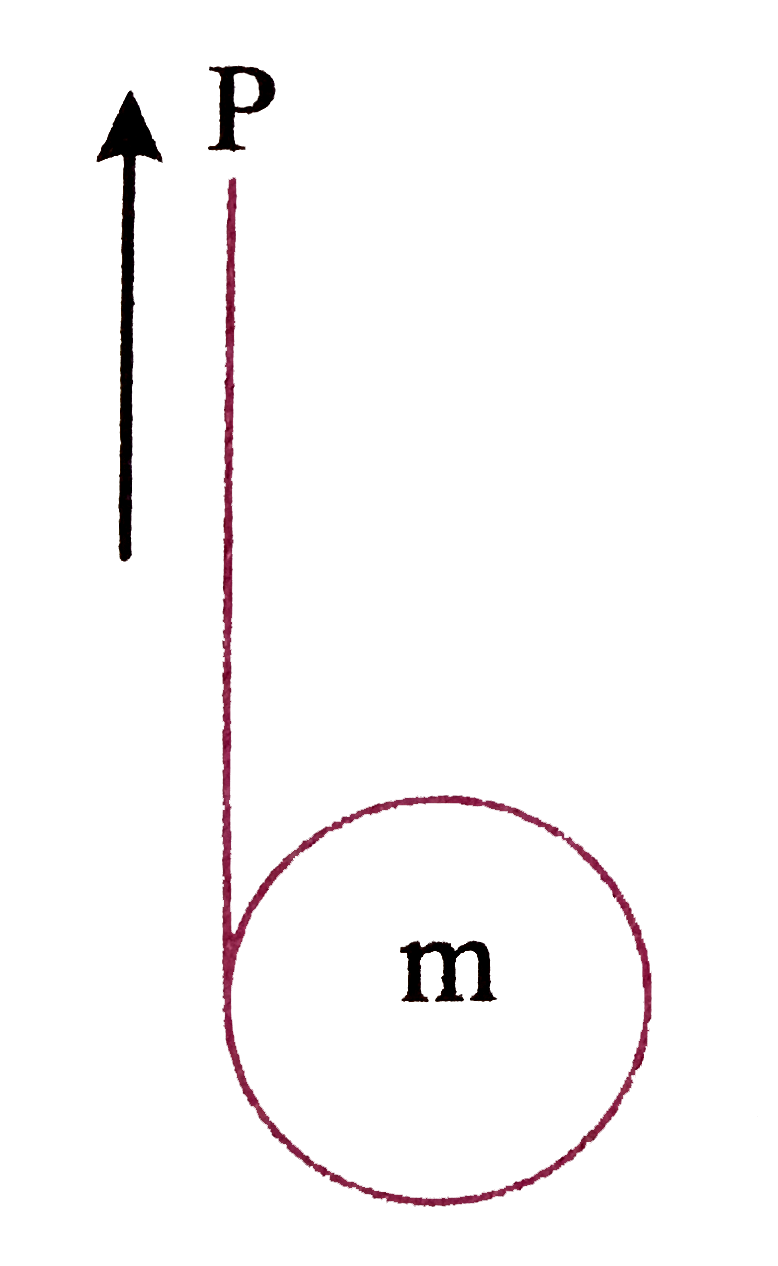Home
Class 11
PHYSICS
The point P of a string is pulled up wit...

The point `P` of a string is pulled up with an acceleration `g`. Then the acceleration of the hanging disc (w.r.t ground) over which the string is wrapped, is

A

`(2 g)/3 darr`

B

`g/3 uarr`

C

`(4g)/3 darr`

D

`g/3 darr`

Text Solution

Verified by Experts

The correct Answer is:
D
`2mg-T=ma, TR=Ialpha`
`alpha=a/R,`solving `alpha=g/3`
Promotional Banner

Topper's Solved these Questions

  • SYSTEM OF PARTICLES

    NARAYNA|Exercise Level-V|72 Videos

  • PHYSICAL WORLD

    NARAYNA|Exercise C.U.Q|10 Videos

  • SYSTEM OF PARTICLES AND ROTATIONAL MOTION

    NARAYNA|Exercise EXERCISE - IV|39 Videos

Similar Questions

Explore conceptually related problems

Find the acceleration of C w.r.t. ground.

If block A is moving with an acceleration of 5ms^(-2) , the acceleration of B w.r.t. ground is

A body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a fuction of the distance measured from the mass M (bottom of the string).

One end of a string of length L is tied to the ceiling of a lift accelerating upwards with an acceleration 2. The other end o the string is freee. The linear mass density of the string varies linearly from 0 to lamda from bottom to top. The acceleration of a wave pulled through out the string is (pg)/(4) . Find p.

In the Fig. shown pulley moves with acceleration vec(v)_(P) . Let acceleration of blocks m_(1) and m_(2) w.r.t. ground are vec(v)_(1) and

A block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g//3 . The work done by the string is

A pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration 'a' the tension in the string is T_(1) . When the elevator moves down with the same acceleration, the tension in the string is T_(2) . If the elevator were stationary, the tension in the string would be

A rod touches a disc kept on a smooth horizontal plane. If the rod moves with an acceleration a , the disc rolls on the rod without acceleration a , the disc rools on therod without slidding. Then , the acceleration of the disc w.r.t the rod is

Knowledge Check

  • If block A is moving with an acceleration of 5ms^(-2) , the acceleration of B w.r.t. ground is

    A
    `5ms^(-2)`
    B
    `5sqrt(2)ms^(-2)`
    C
    `5sqrt(5)ms^(-2)`
    D
    `10ms^(-2)`

  • A block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g//3 . The work done by the string is

    A
    `(mgd)/(3)`
    B
    `(-mgd)/(3)`
    C
    `(2)/(3)mgd`
    D
    `(-2)/(3)mgd`

  • A pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration 'a' the tension in the string is T_(1) .When the elevator moves down with the same acceleration, the tension in the string is T_(1) .If the elevator were stationary, the tension in the string would be

    A
    `(T_(1)+T_(2))/(2)`
    B
    `sqrt(T_(1)+T_(2))`
    C
    `(T_(1)T_(2))/(T_(1)+T_(2))`
    D
    `(2T_(1)T_(3))/(T_(1)+T_(2))`
    • NARAYNA-SYSTEM OF PARTICLES-Level-VI
    1. The point P of a string is pulled up with an acceleration g. Then the ...

      Text Solution

      |

    2. A plank of mass M is placed over smooth inclined plane and sphere is a...

      Text Solution

      |

    3. Four beads each of mass m are glued at the top, bottom and the ends of...

      Text Solution

      |

    4. A rolling body is connected with a trolley car by a spring of stiffne...

      Text Solution

      |

    5. A linear impulse int Fdt acts at a point C of the smooth rod AB. The v...

      Text Solution

      |

    6. Two light vertical springs with equal natural length and spring consta...

      Text Solution

      |

    7. Ler l be the moment of inertia of a uniform square plate about an axi...

      Text Solution

      |

    8. Two point masses A of mass M and B of mass of 4M are fixed at the ends...

      Text Solution

      |

    9. A conical pendulum consists of a mass M suspended from a string of len...

      Text Solution

      |

    10. A ring of mass m and radius R is rolling down on a rough inclined plan...

      Text Solution

      |

    11. A ring of mass M and radius R lies in x-y plane with its centre at ori...

      Text Solution

      |

    12. As shown in figure, the hinges A and B hold a uniform 400N door in pla...

      Text Solution

      |

    13. Find minimum height of the obstacle so that the shpere can stay in equ...

      Text Solution

      |

    14. In the figure shown, suppose the compound pulley and the disc have the...

      Text Solution

      |

    15. Two identical rings A and B are acted upon by torques tau(A) and tau(B...

      Text Solution

      |

    16. A uniform solid sphere of radius r is rolling on a smooth horizontal s...

      Text Solution

      |

    17. Angular acceleration of the cylinder C shows in the figure is (all str...

      Text Solution

      |

    18. A particle of mass m is released from rest at point A in the figure fa...

      Text Solution

      |

    19. The end B of the rod AB which makes angle theta with the floor is bein...

      Text Solution

      |

    20. A block having equilateral triangular cross-section of side a and mass...

      Text Solution

      |