Given-Mass of each block `A` and `b, m = 0.1kg` Radius of circle, `R = 0.06m`
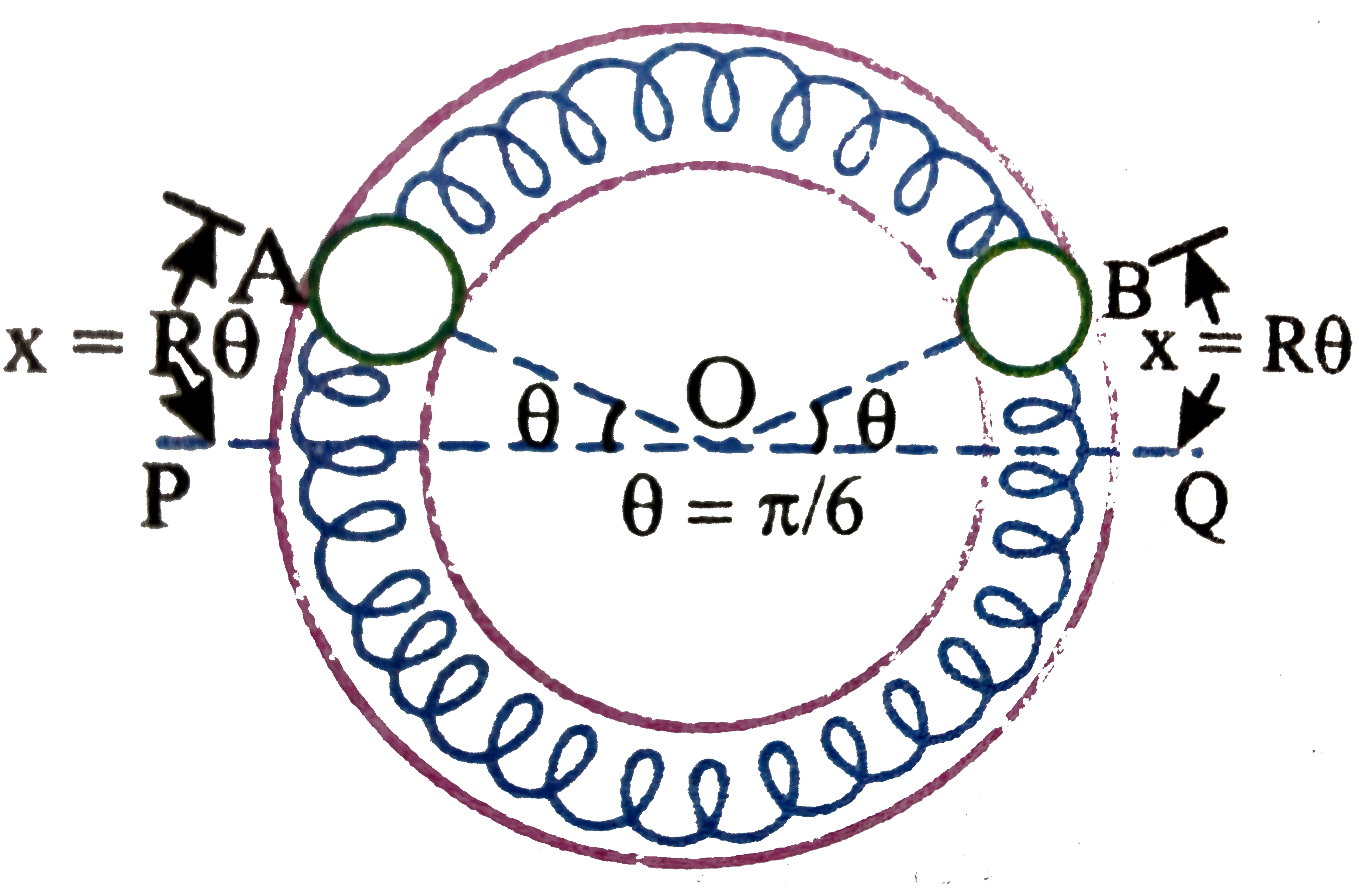
Natural length of spring `l_(0) = 0.06 pi = piR` (Half circle) and spring constant, `k = 0.1N//m` In the streteched position elongation in each spring `x =R theta`. Let us draw `FBD` of `A`
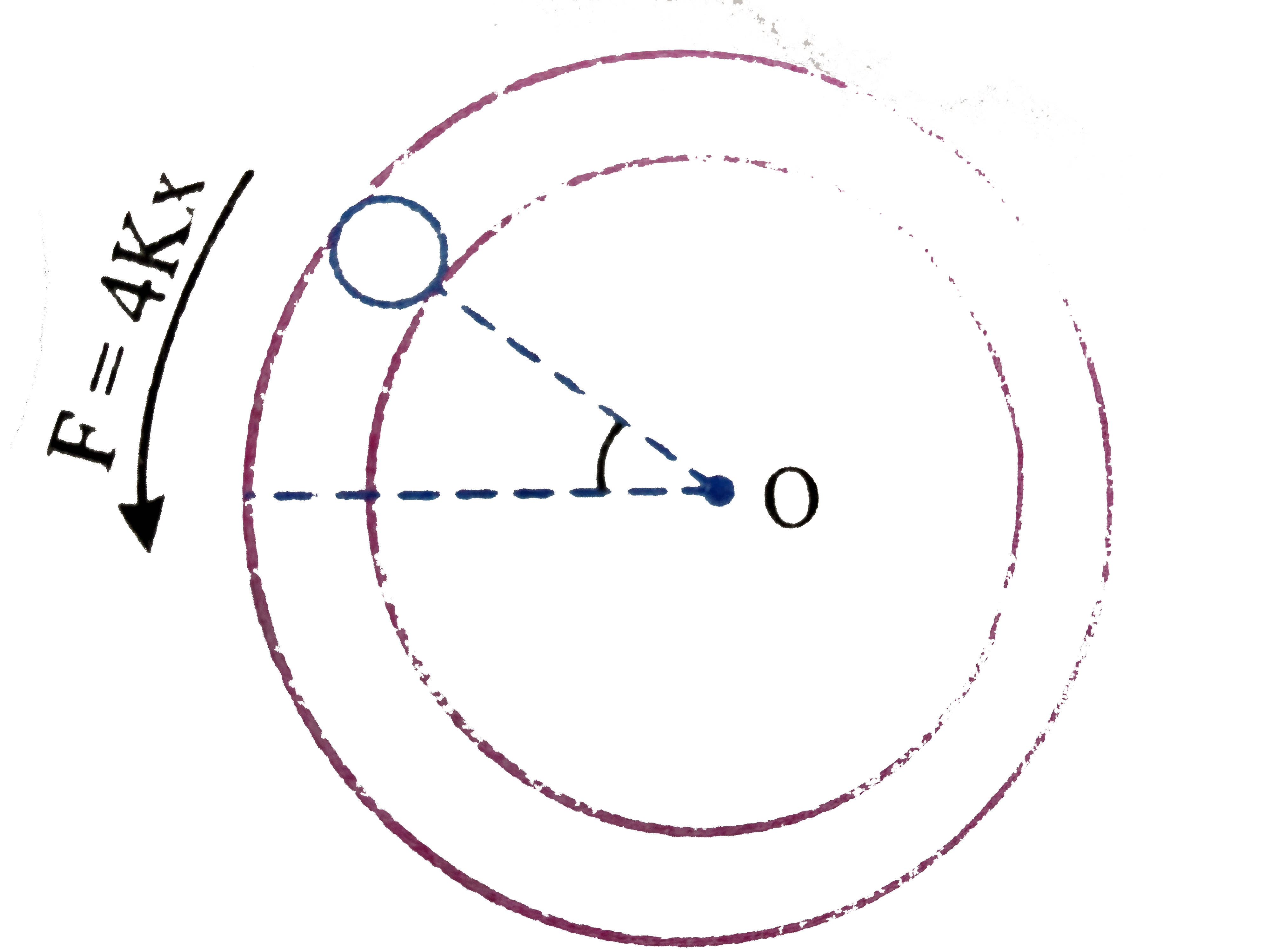
Spring in lower side is stretched by `2x` and on upper side compressed by `2x`. Therefore, each spring will exert a force `2kx` on each block. Hence, a restroing force, `F =5kx` will acr on `A` in the direction shown in figure.
`tai =- F.R =-(4kx)R =- (4kR theta) R or tau =- 4kR^(2). theta(1)`
Since, each ball executes angular `SHM` about origin `O`. Eq. (1) can be rewritten as
`I alpha =- 4 kR^(2) q or (mR^(2))alpha =- 4kR^(2) theta or alpha =- ((4k)/(m)) theta`
`:.` Frequency oscillation, `f = (1)/(2pi) sqrt(|("acceleration")/("displacement")|)=(1)/(2pi)sqrt(|(alpha)/(theta)|)`
`f = (1)/(2pi) sqrt((4k)/(m))` Substituting the values, we hae
`f = (1)/(2pi) sqrt((4xx0.1)/(0.1)) =(1)/(pi) Hz`
(ii) In stretched position, potential energy of the system is `PE =2 {(1)/(2)k} {2x}^(2) =4 kx^(2)` and in mean position, both the blocks have kinetic enegry only.
Hence, `KE = 2 {(1)/(2)mv^(2)} =mv^(2)` From energy conservation
`PE = KE, :. 4 kx^(2) =mv^(2)`
`:. v = 2x sqrt((k)/(m)) = 2R theta sqrt((k)/(m))`
`:. v = 2(0.06) ((pi)/(6)) sqrt((0.1)/(0.1)) or v = 0.0628 m//s`
(iii) Total energy of the sysetm, `E = PE` in stretched position or `=KE` in mean position
`E = mv^(2) =(0.1) (0.0628)^(2) J or E = 3.9 xx 10^(-4)J`