At resonance, `V_(L)` and `V_(C )` both very much greater than the applied potential, `V` itself. The quantity factor for an `LCR` circuit in resonance is given by `Q = (X_(L))/(R )`. In pratice, `Q = 200` has been achieved.
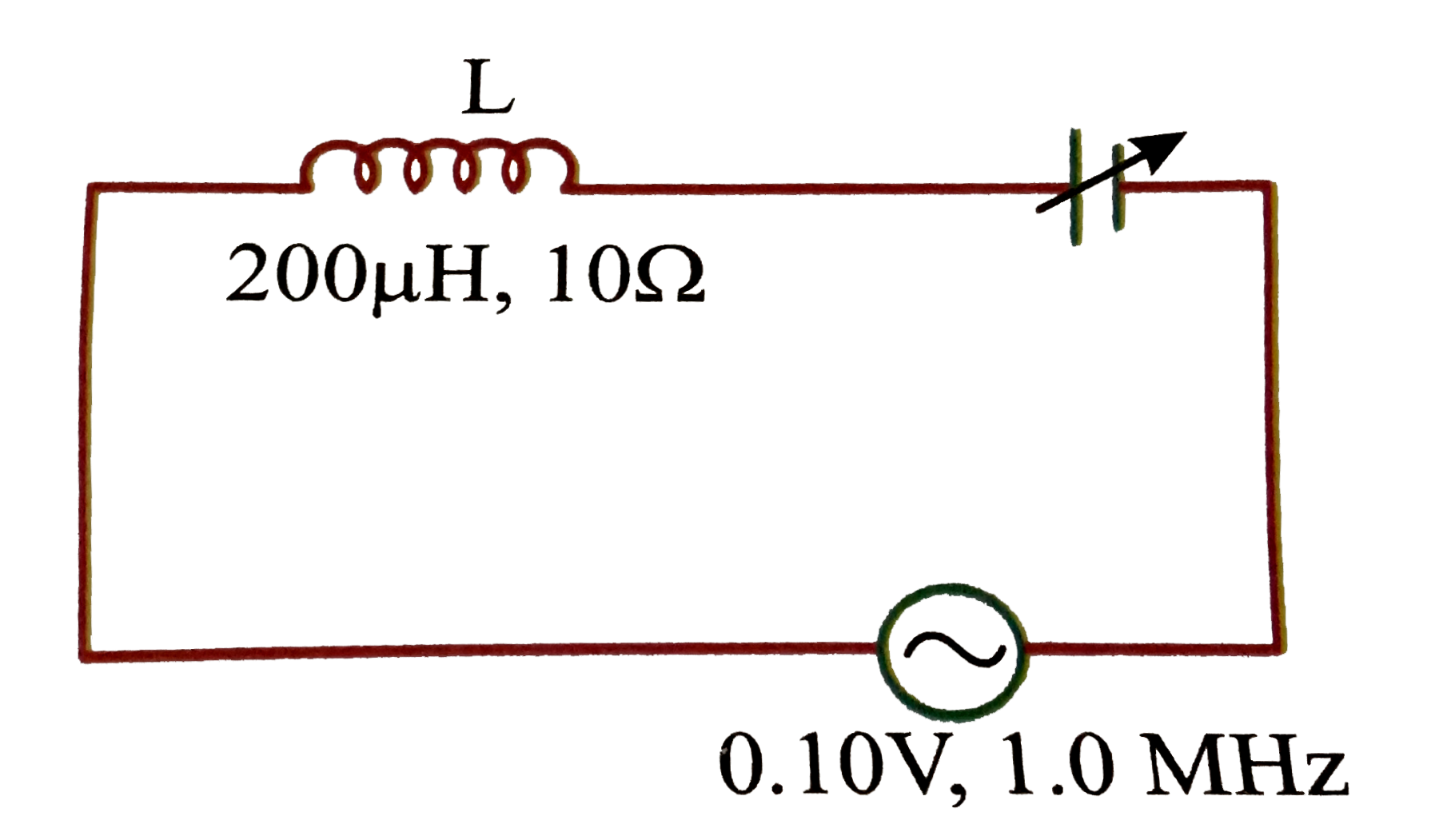
At resonance, the capacitor has been adjusted for
(1). `200 xx 10^(-6) mu F`
(2) `0.00013 mu F`
(3). `0.0012 mu F`
(4). `0.0013 F`
At resonance, the potential difference across the inductance is
(1) `1.3 V`
(2) `13 V`
(3). `0.3 V`
(d) none of these
The potential across the capacitor at resosnance is
(1) `1.3 V`
(2) `13 V`
(3) `lt 13 V`
(4) none of these
The `Q` factor is
(1) `(V_(L))/(V_(C ))`
(2) `(V_(C ))/(V_(L))`
(3) `(V_(C ))/(V)`
(d) `(V_(L))/(V)`
(e) choose the right statement.
(1) `V_(L)+V_(C)` can be greater than `V_("applied")`
(2) `V_(L)+V_(C)=V_("applied")`
(3) `V_(L)+V_(C) lt V_("applied")`
(4) none of these