Home
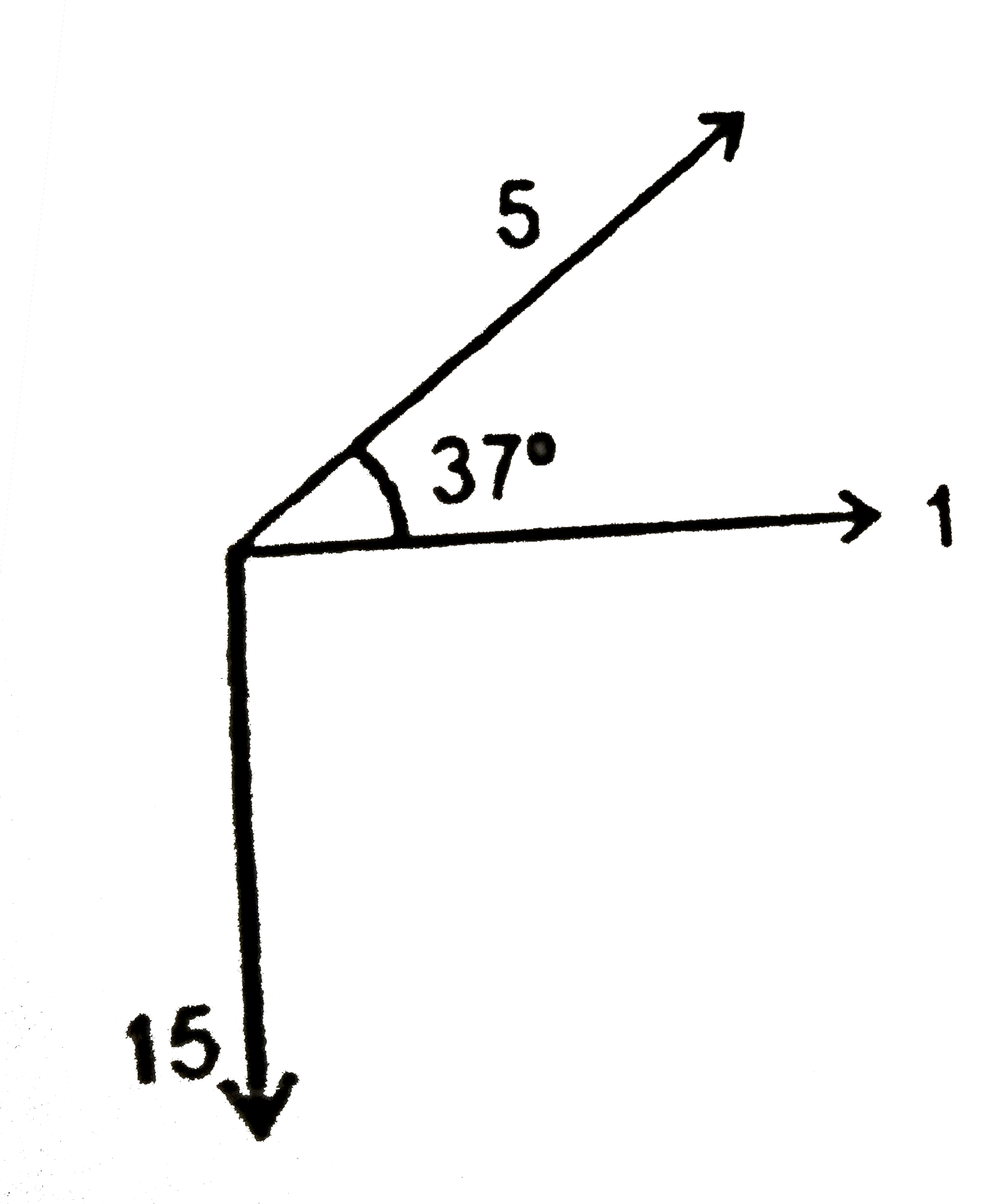
Class 11
PHYSICS
The resultant amplitude due to super pos...

The resultant amplitude due to super position of `x_(1)=sin omegat, x_(2)=5 sin (omega t +37^(@))` and `x_(3)=-15 cos omega t ` is `:`

A

17

B

21

C

13

D

None of these

Text Solution

Verified by Experts

The correct Answer is:
C
`x_(1)=sin omegat,x_(2)=5 sin ( omegat+37^(@))`
`x_(3)=15 sin ( omegat-pi//2)`
By the phasor diagram `,`

Get the resultant of these 3 vectors as 13.
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise DPP 77|8 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 78|3 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 75|5 Videos

  • CURRENT ELECTRICITY

    RESONANCE|Exercise Exercise|54 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

The resultant amplitude due to superposition of three simple harmonic motions x_(1) = 3sin omega t , x_(2) = 5sin (omega t + 37^(@)) and x_(3) = - 15cos omega t is

x_(1) = 3 sin omega t x_(2) = 5 sin (omega t + 53^(@)) x_(3) = - 10 cos omega t Find amplitude of resultant SHM.

Find the resultant amplitude of the following simple harmonic equations : x_(1) = 5sin omega t x_(2) = 5 sin (omega t + 53^(@)) x_(3) = - 10 cos omega t

The amplitude of the vibrating particle due to superposition of two SHMs , y_(1)=sin (omega t+(pi)/(3)) and y_(2)=sin omega t is :

Find the displacement equation of the simple harmonic motion obtained by combining the motion. x_(1) = 2sin omega t , x_(2) = 4sin (omega t + (pi)/(6)) and x_(3) = 6sin (omega t + (pi)/(3))

If i_(1) = 3 sin omega t and i_(2) =6 cos omega t , then i_(3) is

If i_(1)=3 sin omega t and (i_2) = 4 cos omega t, then (i_3) is

The ratio of amplitudes of following SHM is x_(1) = A sin omega t and x_(2) = A sin omega t + A cos omega t