Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.33|20 VideosView PlaylistDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.34|9 VideosView PlaylistDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.31|20 VideosView PlaylistCURRENT ELECTRICITY
RESONANCE|Exercise High Level Problems (HIP)|21 VideosView PlaylistELECTRO MAGNETIC WAVES
RESONANCE|Exercise Exercise 3|27 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEM-DPP No.32
- A car is moving along a circle with constant speed on an inclined pla...
02:36
|
Play - A block of density 2000kg//m^3 and mass 10kg is suspended by a spring ...
02:35
|
Play - A horizontal cylinder is fixed, its inner surface is smooth and its ra...
02:07
|
Play - A chain of mass 'm' and radius 'r' is placed onto a cone of semi verti...
08:12
|
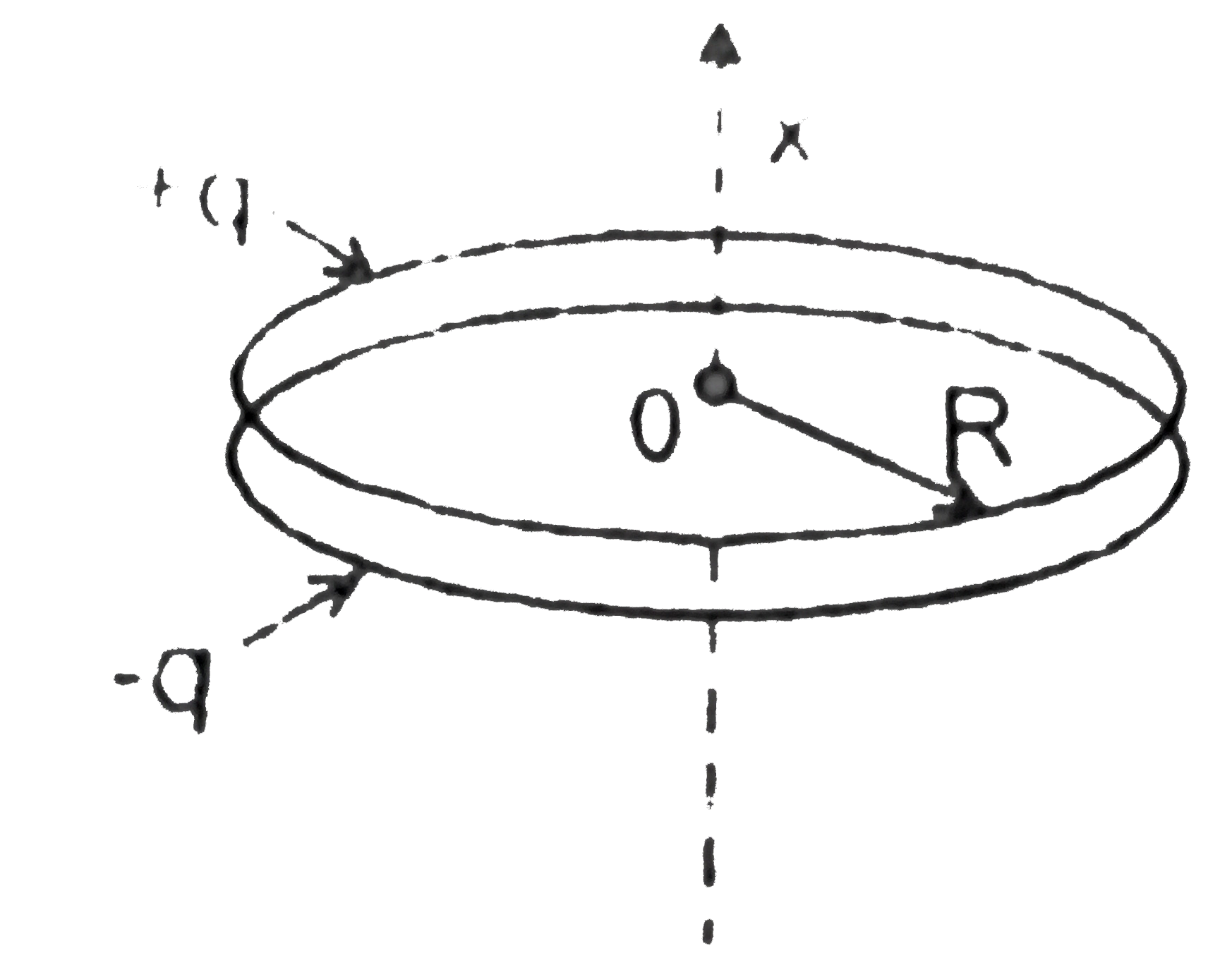
Play - Two coaxial rings, eacg of radius R, made of thin wire are separated b...
02:52
|
Playing Now - An infinitely large non-conducting plane of uniform surface charge den...
07:45
|
Play - A tank of height H and base area A is half filled with water and there...
05:58
|
Play - A tank of height H and base area A is half filled with water and there...
05:58
|
Play - A tank of height H and base area A is half filled with water and there...
05:58
|
Play