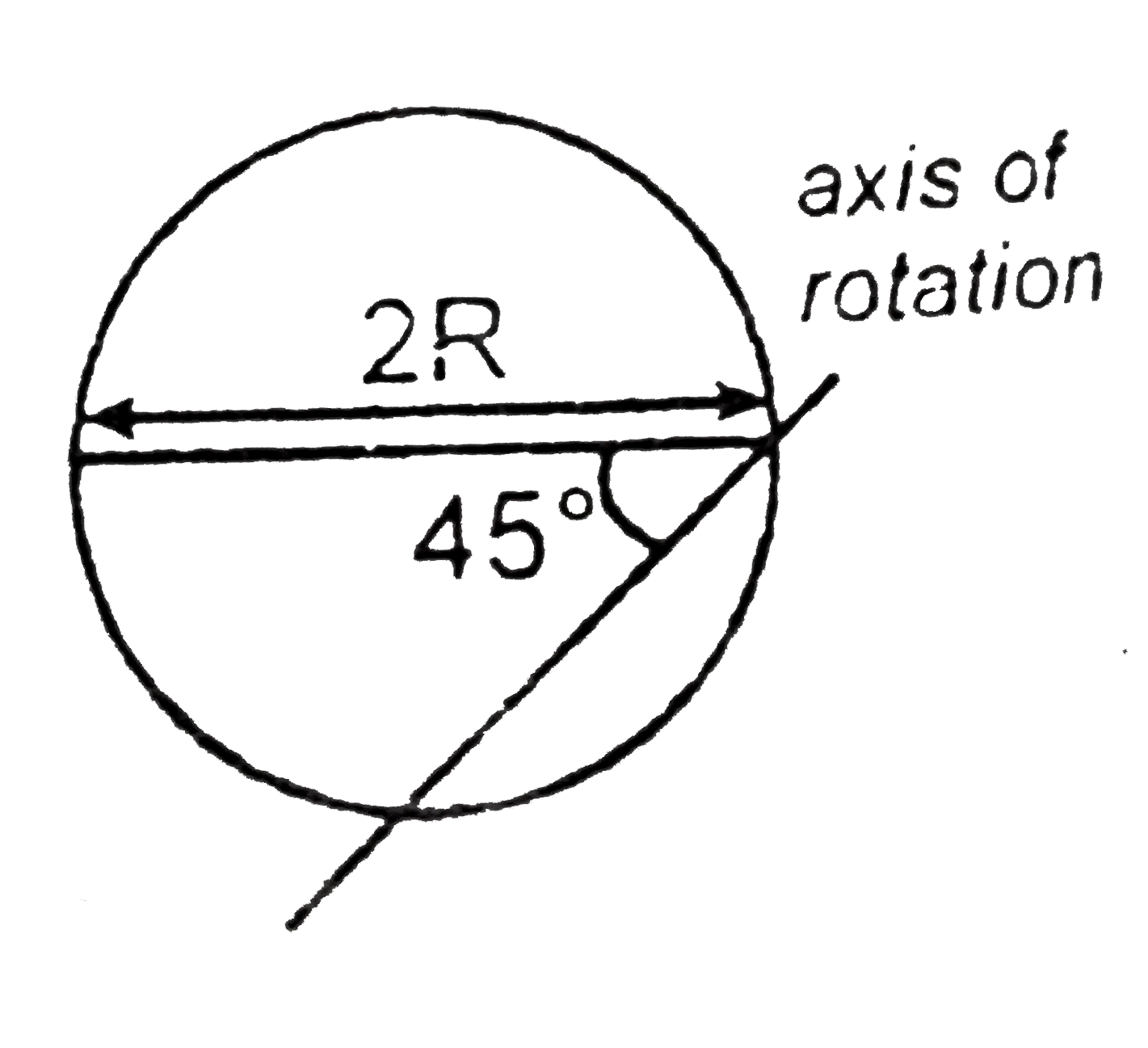A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.59|9 VideosView PlaylistDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.60|9 VideosView PlaylistDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.57|9 VideosView PlaylistCURRENT ELECTRICITY
RESONANCE|Exercise High Level Problems (HIP)|21 VideosView PlaylistELECTRO MAGNETIC WAVES
RESONANCE|Exercise Exercise 3|27 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEM-DPP No.58
- In the circuit shown in fig. X(C ) = 100 Omega,(XL)=200 Omega and R=10...
03:32
|
Play - If for above circuit the capacitive reactance is two times of inductiv...
04:25
|
Play - In YDSE shown in figure a parallel beam of light is incident on the sl...
03:23
|
Play - What will be the angle of diffracting for the first minimum due to Fra...
01:59
|
Play - A solid ball of mass m and radius R is released from the position show...
02:36
|
Play - Two particles A and B masses 1 kg and 2 kg respectivelty are projected...
05:32
|
Play - Two balls of same mass are released simultaneously from heights h & 2h...
06:05
|
Play - The graph in the figure shows how the displacement of a particle descr...
03:50
|
Play - The moment of inertia of a uniform thin rod of mass m and length L abo...
02:22
|
Playing Now - In a hydrogen atom following Bohr's postulates , the product of linear...
01:49
|
Play - The moment of inertia of a thin sheet of mass M of the given shape abo...
Text Solution
|
Play - Particle 'A' moves with speed 10m//s in a frictionless circular fixed ...
03:26
|
Play - In single slit diffraction pattern :
01:23
|
Play - A liquid is contained in a vertical tube of semi-circular cross-sectio...
01:38
|
Play - Two semicircular rings of linear mass densities lamda and 2 lamda and ...
02:36
|
Play - Figure above shows a closed Gaussian surface in the space of a cube of...
06:05
|
Play - Two wires each of radius of cross section r but of different materials...
01:46
|
Play - A piece of copper wire has twice the radius of a piece of steel wire....
05:45
|
Play - A small block of mass 'm' is placed on bigger block of mass M(1) which...
04:15
|
Play - A beaker is filled with water as shown in figure (a). The bottom surfa...
03:23
|
Play