Home
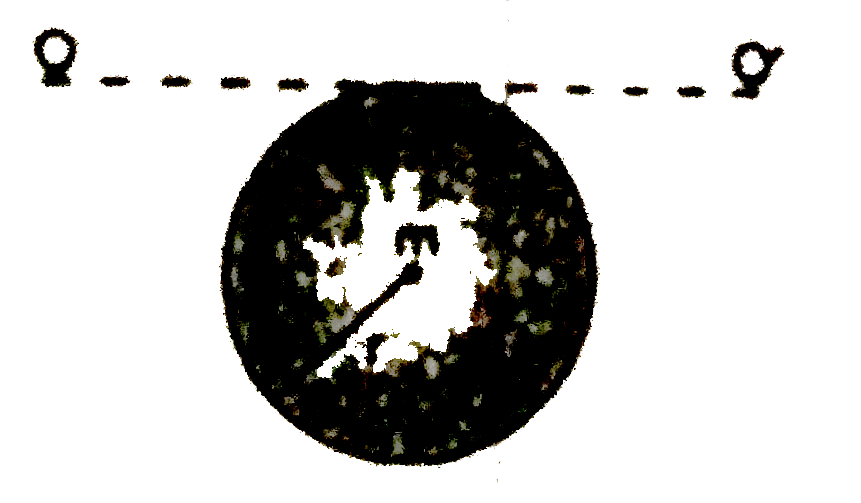
Class 11
PHYSICS
Moment of inetia of a disc about OO' is...

Moment of inetia of a disc about OO' is

A

`(3mr^(2))/2`

B

`(mr^(2))/2`

C

`(5mr^(2))/2`

D

`(5mr^(2))/4`

Text Solution

Verified by Experts

The correct Answer is:
D
`I_(AB)=(mr^(2))/4` (by perpendicular axis theorem) by applying parallel axis theorem
`I_(0,0)=(mr^(2))/4+mr^(2)=(5mr^(2))/4`
Promotional Banner

Topper's Solved these Questions

Similar Questions

Explore conceptually related problems

Moment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R . The value of x is

Moment of inertia of a disc about an axis which is tangent and parallel to its plane is I . Then the moment of inertia of disc about a tangent, but perpendicular to its plane will be

Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is

Calculate the moment of inertia of a disc about its any diameter ?

The Moment of inertia of a disc about an axis passing through its centre and perpendicular to its plane is 1 / 2 MR^2 . Derive the values of moment of inertia of the disc about its diameter and about an axis tangential to the disc lying on its plane ?

Moment of inertia of a disc about an axis passing through its centre and perpendicular to its plane is frac (1)(2)MR^2 . Determine the moment of inertia of this disc about its diameter and about a tangent perpendicular to its plane.

The moment of intertia of a disc about an axis passing through its centre and normal to its plane is I. The disc is now folded along a diameter such that the two halves are mutually perpendicular. Its moment of inertia about this diameter will now be

Mass of bigger disc having radius 2R is M. A disc of radius R is cut from bigger disc. Moment of intertia of disc about an axis passing through periphery and perpendicular to plane is

Assuming he expression for the moment of inertia of a thin disc about its diameter, show that the moment of inertia of the disc about a tangent in its plane is (5)/(4)MR^(2)

RESONANCE-RIGID BODY DYNAMICS-Exercise
  1. Moment of inetia of a disc about OO' is

    Text Solution

    |

  2. Three point masses are arranged as shown in the figure. Moment of iner...

    Text Solution

    |

  3. A thin wire of length L and uniform linear mass density rho is bent in...

    Text Solution

    |

  4. Three identical rods, each of length L, are joined to form a rigid equ...

    Text Solution

    |

  5. Three rings, each of mass m and radius r, are so placed that they touc...

    Text Solution

    |

  6. The moment of inertia of a door of mass m, length 2 l and width l abou...

    Text Solution

    |

  7. Two light vertical springs with equal natural length and spring consta...

    Text Solution

    |

  8. A uniform rod of mass m and length L is suspended with two massless st...

    Text Solution

    |

  9. Two persons of equal heights are carrying a long uniform wooden plank ...

    Text Solution

    |

  10. A force vec(F)=4hati-10 hatj acts on a body at a point having position...

    Text Solution

    |

  11. A uniform rod of length L and weight W(R) is suspended as shown in the...

    Text Solution

    |

  12. Two points of a rod move with velocity 3 v and v perpendicular to the...

    Text Solution

    |

  13. A rod can rotate in a horizontal plane about its one end. A bead which...

    Text Solution

    |

  14. In the pulley system shown, if radii of the bigger and smaller pulley ...

    Text Solution

    |

  15. A rod of mass m and length l is kept on a surface that has no friction...

    Text Solution

    |

  16. If vec(tau)xxvec(L)=0 for a rigid body, where vec(tau)= resultant torq...

    Text Solution

    |

  17. A smooth tube of certain mass is rotated in a gravity-free Space and r...

    Text Solution

    |

  18. A smooth sphere A is moving on a frictionless horizontal plane with an...

    Text Solution

    |

  19. A body of mass m and radius r is rotated with angular velocity omega a...

    Text Solution

    |

  20. A uniform circular disc of radius r is placed on a rough horizontal su...

    Text Solution

    |