A metal cylinder of length L and radius R is fixed rigidly to ground with its axis vertical. A twisting torque `tau_(0)` is applied along the circumference at the top of the cylinder. This causes an angular twist of `theta_(0)` (rad) in the top surface. Calculate the shear modulus of elasticity `(eta)` of the material of the cylinder.
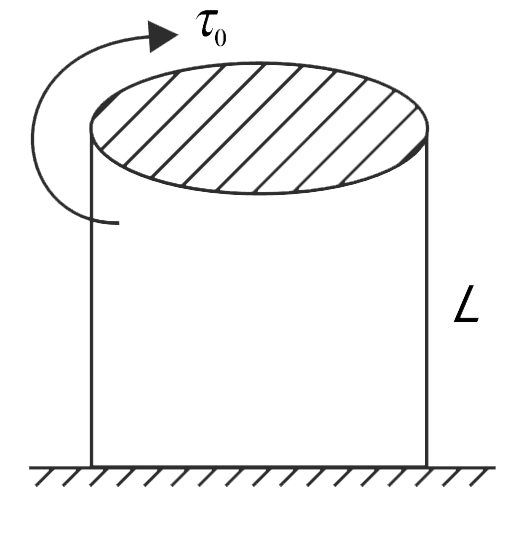
A metal cylinder of length L and radius R is fixed rigidly to ground with its axis vertical. A twisting torque `tau_(0)` is applied along the circumference at the top of the cylinder. This causes an angular twist of `theta_(0)` (rad) in the top surface. Calculate the shear modulus of elasticity `(eta)` of the material of the cylinder.
Text Solution
Verified by Experts
The correct Answer is:
`(2l tau_(0))/(pi R^(4) theta_(0))`
|
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
Consider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll the plank always remains horizontal. there is no slipping at any point of contact. Calculate the acceleration of the cylinder and the frictional forces at the two contact.
Knowledge Check
A hollow cylinder of length L and radius R having surface area A is placed horizontally with its axis parallel to an external field E. The electric flux through the surface of the cylinder is
A hollow cylinder of length L and radius R having surface area A is placed horizontally with its axis parallel to an external field E. The electric flux through the surface of the cylinder is
A
Zero
B
`2piRLE`
C
`2 piR^2E`
D
E . A
A hollow cylinder of length L and radius R having surface area A is placed horizontally with its axis parallel to an external field E. The electric flux through the surface of the cylinder is
A hollow cylinder of length L and radius R having surface area A is placed horizontally with its axis parallel to an external field E. The electric flux through the surface of the cylinder is
A
Zero
B
`2piRLE`
C
`2 piR^2E`
D
E . A
A fixed thermally conducting cylinder has a radius R and height L_0 . The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P_0 . The piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brought below the cylinder and put in a position so that the water surface in the tank is at the same level as the top of the cylinder as shown in the figure. The density of the water is rho . In equilibrium, the height H of the water coulmn in the cylinder satisfies
A fixed thermally conducting cylinder has a radius R and height L_0 . The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P_0 . The piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brought below the cylinder and put in a position so that the water surface in the tank is at the same level as the top of the cylinder as shown in the figure. The density of the water is rho . In equilibrium, the height H of the water coulmn in the cylinder satisfies
A
`rhog(L_0-H)^2+P_0(L_0-H)+L_0P_0=0`
B
`rhog(L_0-H)^2-P_0(L_0-H)-L_0P_0=0`
C
`rhog(L_0-H)^2+P_0(L_0-H)-L_0P_0=0`
D
`rhog(L_0-H)^2-P_0(L_0-H)+L_0P_0=0`
Similar Questions
Explore conceptually related problems
A rectangular rigid fixed block has a long horizontal edge. A solid homogeneous cylinder of radius R is placed horizontally at rest with its length parallel to the edge such that the axis of the cylinder and the edge of the block are in the same vertical plane as shown in figure. there is sufficient friction present at the edge so that so that a very small displacement cause the cylinder to roll of the edge without slipping. Determine (a) the angle theta_(C) through which the cylinder rotates before it leaves contact with the edge, (b) the book of the centre of mass of the cylinder before leaving contact with the edge, and ( c) the ratio of the translational to rotational kinetic energyies of the cylinder when its centre of mass is in horizontal line with the edge. .
A uniform solid cylinder of density 0.8g//cm^3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical. The densities of the liquids A and B are 0.7g//cm^3 and 1.2g//cm^3 , respectively. The height of liquid A is h_A=1.2cm. The length of the part of the cylinder immersed in liquid B is h_B=0.8cm . (a) Find the total force exerted by liquid A on the cylinder. (b) Find h, the length of the part of the cylinder in air. (c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.
A uniform cylinder of radius r and mass m can rotate freely about a fixed horizontal axis. A thin cord of length l and mass m_(0) is would on the cylinder in a single layer. Find the angular acceleration of the cylinder as a function of the length x of the hanging part of the end. the wound part of the cord is supposed to have its centre of gravity on the cylinder axis is shown in figure.
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad/s. The radius of the cylinder is 0.25 m. The kinetic energy associated with the rotation of the cylinder is
A soild cylinder of mass 2 kg and radius 0.2 m is rotating about its owm axis without friction with an angular velocity of 3 rad s^(-1) . Angular momentum of the cylinder is