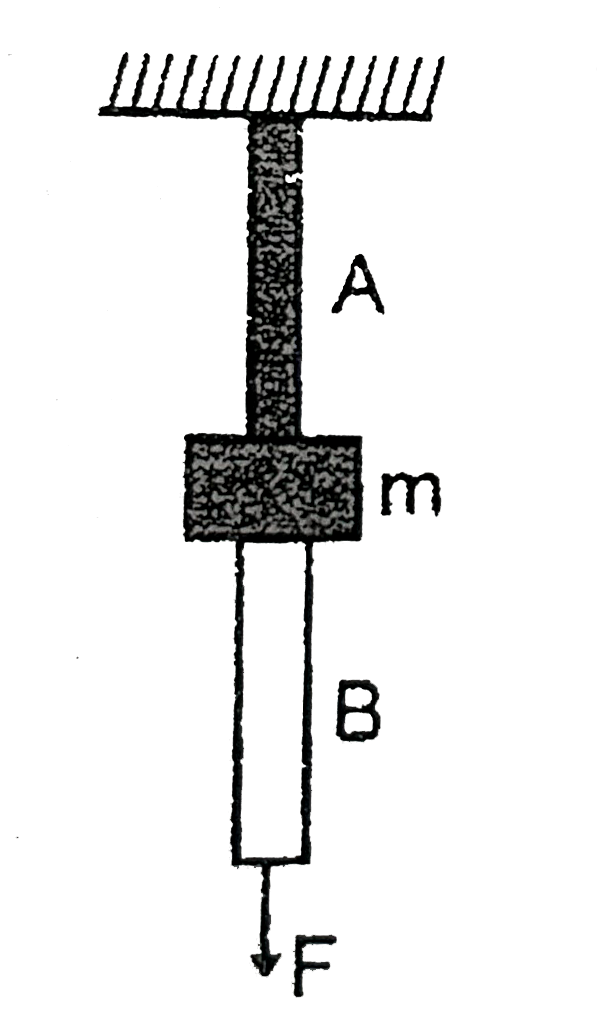A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ELASTICITY AND VISCOCITY
RESONANCE|Exercise Exercise- 3 PART - I|7 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Exercise- 3 PART - IV|9 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Exercise- 2 PART - II|8 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 92 illustration|2 VideosELECTROMAGNETIC INDUCTION
RESONANCE|Exercise Exercise|43 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-ELASTICITY AND VISCOCITY-Exercise- 2 PART - III
- The wires A and B shown in the figur, are made of the same material an...
Text Solution
|
- When a tensile or compressive load 'P' is applied to rod or cable, its...
Text Solution
|
- When a tensile or compressive load 'P' is applied to rod or cable, its...
Text Solution
|
- When a tensile or compressive load 'P' is applied to rod or cable, its...
Text Solution
|
- When a tensile or compressive load 'P' is applied to rod or cable, its...
Text Solution
|
- When a tensile or compressive load 'P' is applied to rod or cable, its...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|