Home
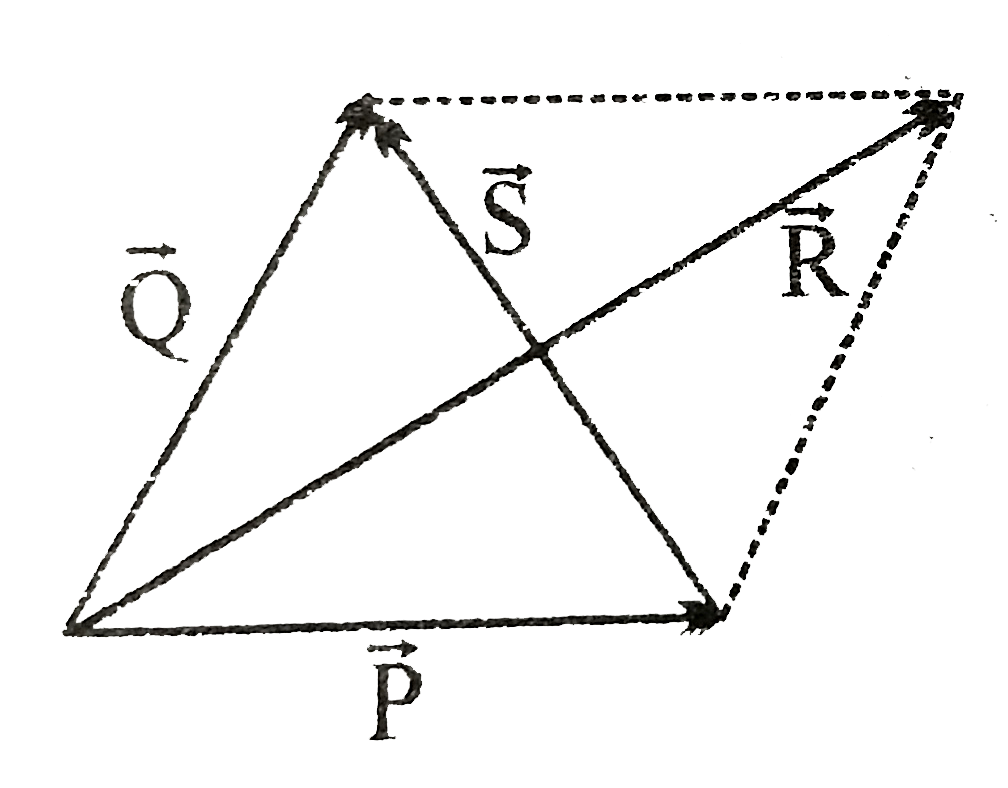
Class 11
PHYSICS
Two vectors vec(P) & vec(Q) are arranged...

Two vectors `vec(P) & vec(Q)` are arranged in such a way that they form adjacent sides of a parallelogram as shown in figure

Which of the following options have correct relationship

A

`vec(Q)=vec(R)+vec(S)`

B

`vec(R)=vec(P)+vec(Q)`

C

`vec(R)=vec(P)+vec(S)`

D

`vec(S)=vec(Q)+vec(P)`

Text Solution

Verified by Experts

The correct Answer is:
B, D
Promotional Banner

Topper's Solved these Questions

  • UNIT DIMENSION, VECTOR & BASIC MATHS

    BANSAL|Exercise EXERCISE-1 [SINGLE CORRECT CHOICE TYPE]|20 Videos

  • UNIT DIMENSION, VECTOR & BASIC MATHS

    BANSAL|Exercise EXERCISE -2 (Miscellaneous Exercise)|13 Videos

  • UNIT DIMENSION, VECTOR & BASIC MATHS

    BANSAL|Exercise Solved Example|17 Videos

  • KINETIC THEORY OF GASES

    BANSAL|Exercise Section-B|13 Videos

Similar Questions

Explore conceptually related problems

Two vectors vec P and vec Q

Vectors vec P and vec Q represent two adjacent sides of a parallelogram.The diagonal of the parallelogram represents:

If vec(A) and vec(B) are two vectors, which of the following is not correct?

If the vector vec(a) lies in the planar of vectors vec(b) and vec(c ) , then which one of the following is correct?

The vector vec(a) lies in the plane of vectors vec(b) and vec(c) . Which one of the following is correct ?

There are two vector vec(A)=3hat(i)+hat(j) and vec(B)=hat(j)+2hat(k) . For these two vectors- (i) Find the component of vec(A) along vec(B) and perpendicular to vec(B) in vector form. (ii) If vec(A) & vec(B) are the adjacent sides of parallelogram then find the magnitude of its area. (iii) Find a unit vector which is perpendicular to both vec(A) & vec(B) .

If vec a and vec b represent two adjacent sides of a parallel then write vectors representing its diagonals.

vec A and vec B are two vectors and theta is the angle between them. If vec A. vec B=0, then which one of the following options is worng ?

If vectors vec a and vec b are two adjacent sides of a parallelogram,then the vector respresenting the altitude of the parallelogram which is the perpendicular to a is vec b+(vec b xxvec a)/(|vec a|^(2)) b.(vec a.vec b)/(|vec b|^(2)) c.vec b-(vec b*vec a)/(|vec a|^(2)) d.(vec a xxvec a))/(|vec b|^(2))

Six vector vec(a) through vec(f) have the magnitudes and direction indicated in the figure. Which of the following statements is true?