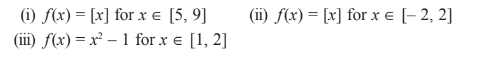Text Solution
Verified by Experts
Topper's Solved these Questions
CONTINUITY AND DIFFERENTIABILITY
NCERT|Exercise EXERCISE 5.5|18 VideosCONTINUITY AND DIFFERENTIABILITY
NCERT|Exercise EXERCISE 5.7|17 VideosCONTINUITY AND DIFFERENTIABILITY
NCERT|Exercise EXERCISE 5.3|15 VideosAPPLICATION OF INTEGRALS
NCERT|Exercise EXERCISE 8.2|7 VideosDETERMINANTS
NCERT|Exercise EXERCISE 4.4|5 Videos
Similar Questions
Explore conceptually related problems
NCERT-CONTINUITY AND DIFFERENTIABILITY-EXERCISE 5.8
- Examine the applicability of Mean Value Theorem for all three functio...
Text Solution
|
- Verify Mean Value Theorem, if f(x)=x^2-4x-3 in the interval [a, b], w...
Text Solution
|
- Verify Mean Value Theorem, if f(x)=x^3-5x^2-3x in the interval [a, b]...
Text Solution
|
- Examine if Rolle's theorem is applicable to any of the following func...
Text Solution
|
- Verify Rolle's theorem for the function f(x)=x^2+2x-8,x in [-4,2].
Text Solution
|
- If f : [-5, 5] to R is a differentiable function and if f^(prime)(x) d...
Text Solution
|