A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
D MUKHERJEE-IIT QUESTIONS 4-Linked -comprehension type
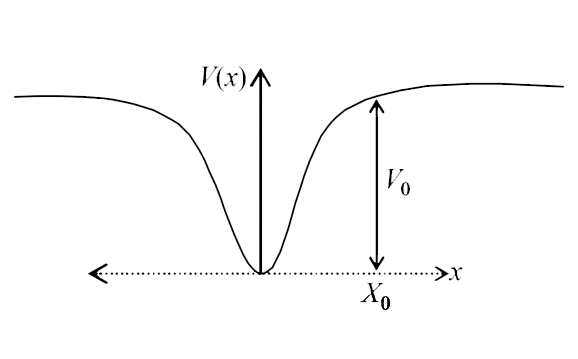
- When a particle of mass m moves on the x-axis in a potential of the fo...
Text Solution
|
- When a particle of mass m moves on the x-axis in a potential of the fo...
Text Solution
|
- When a particle of mass m moves on the x-axis in a potential of the fo...
Text Solution
|
- Electrical resistance of certain materials, known as superconductors, ...
Text Solution
|
- Electrical resistance of certain materials, known as superconductors, ...
Text Solution
|