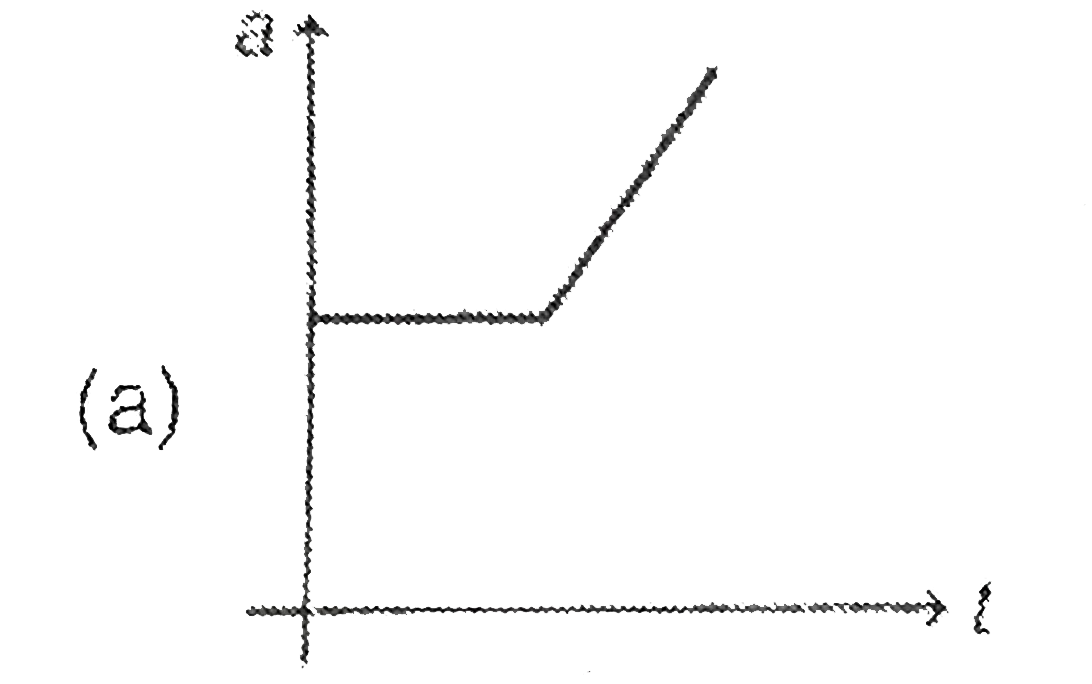
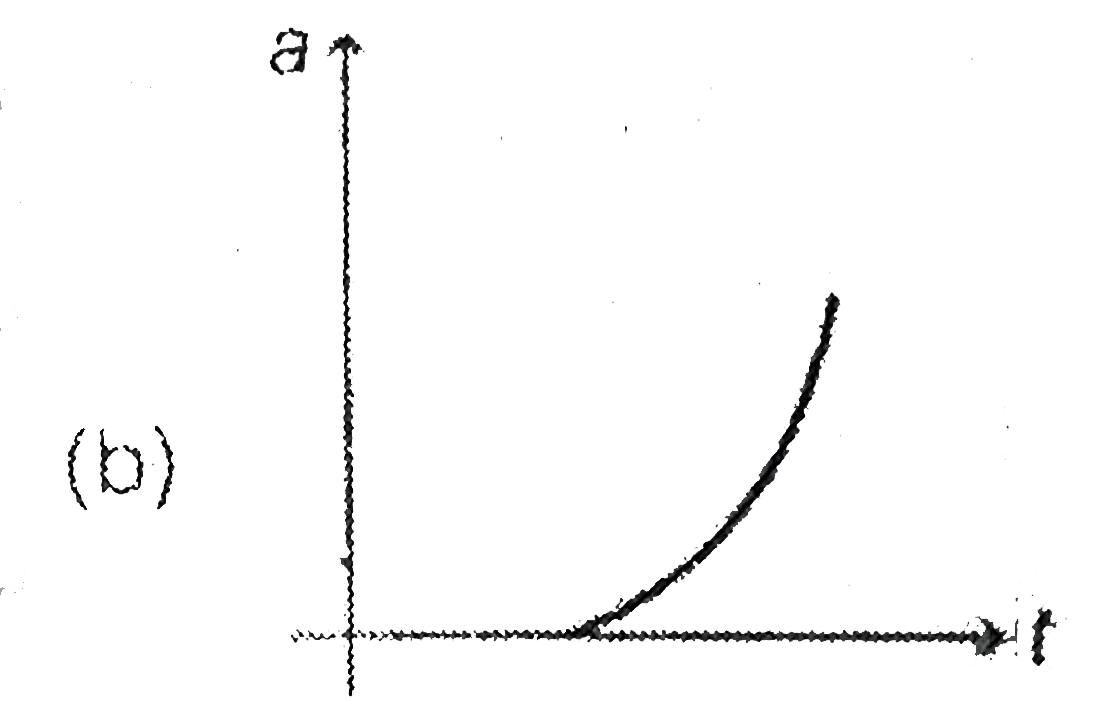
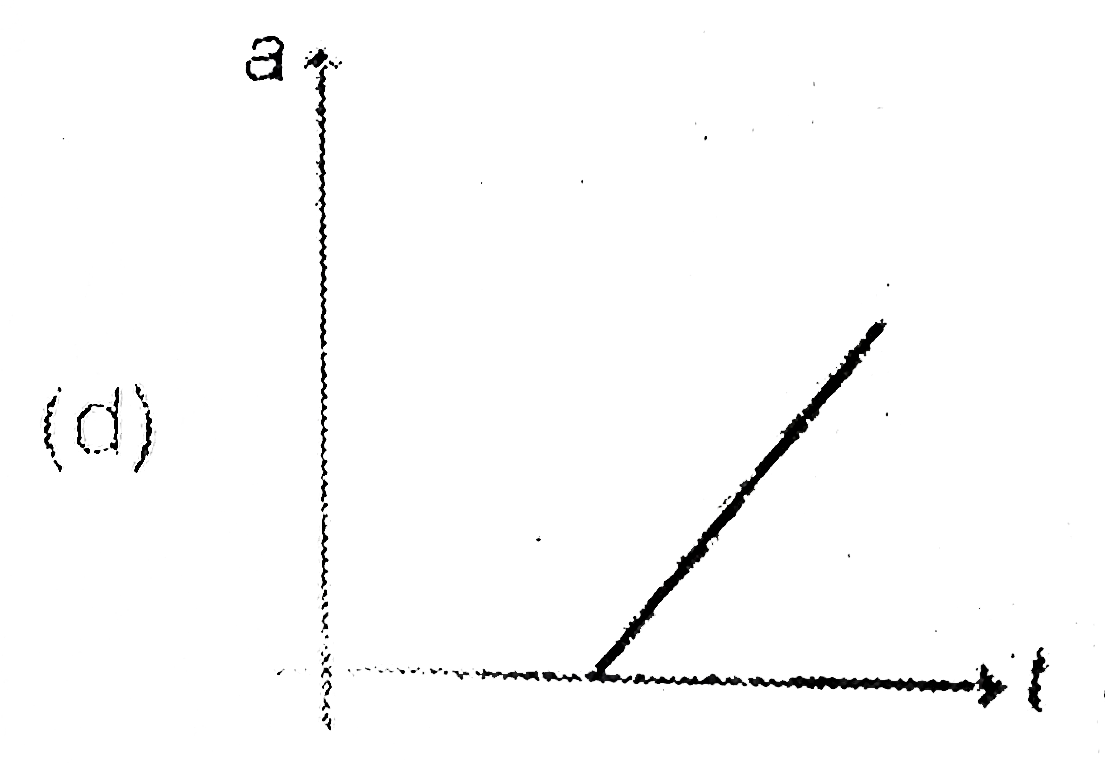
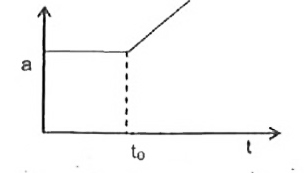
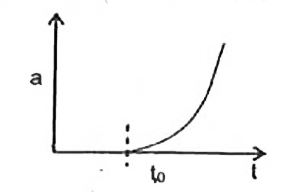
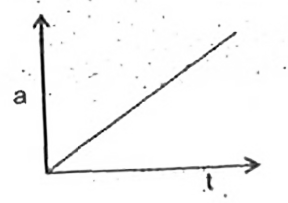
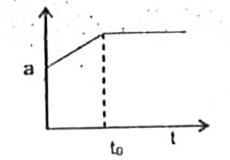
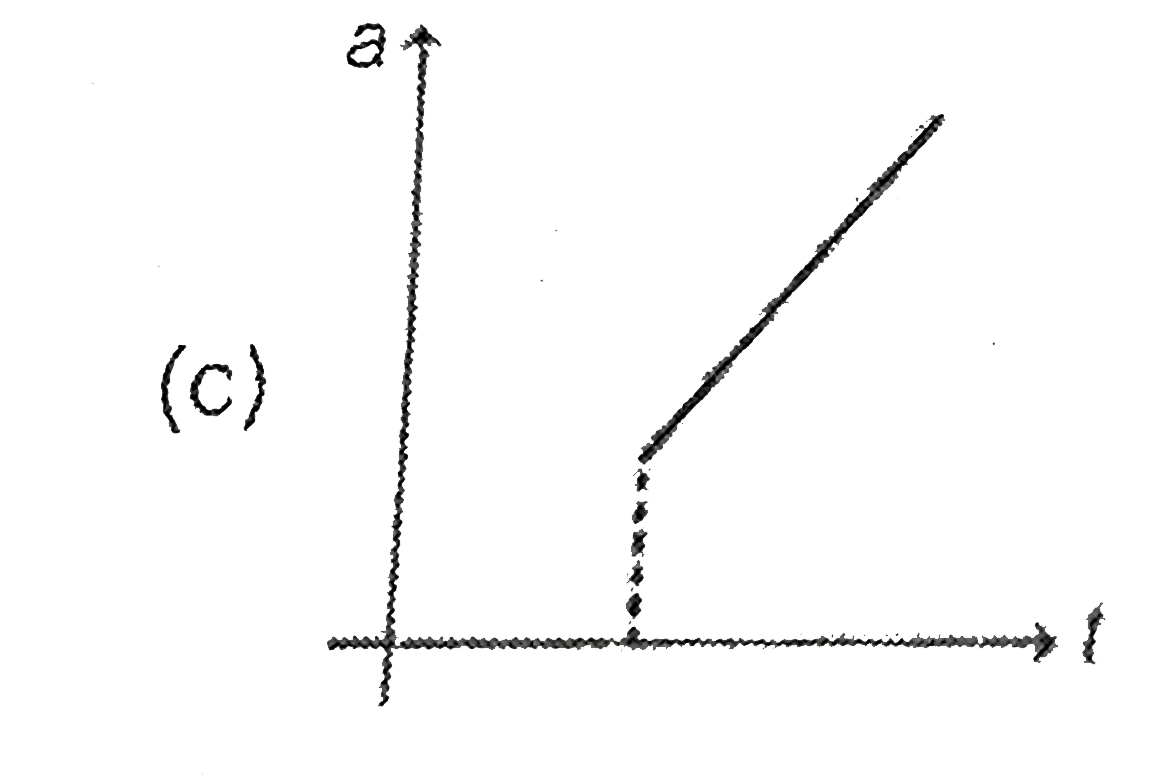A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Knowledge Check
Recommended Questions
- A block is placed on a rough horizontal plane. A time dependent horizo...
Text Solution
|
- A block of mass 4 kg is placed on a rough horizontal force plane. A ti...
Text Solution
|
- A block of mass 4kg is placed on a rough horizontal plane A time depen...
Text Solution
|
- A block of mass 4kg is placed on a rough horizontal plane A time depen...
Text Solution
|
- A block is placed on a rough horizontal plane. A time dependent horizo...
Text Solution
|
- A block is placed on a rough horizontal plane. Three horizontalforces ...
Text Solution
|
- A block is placed on a rough horizontal plane. A time-dependent horizo...
Text Solution
|
- A block of mass 5kg is placed on a rough horizontal plane.A time depen...
Text Solution
|
- A block of mass 4 kg is placed on a rough horizontal plane. A time dep...
Text Solution
|