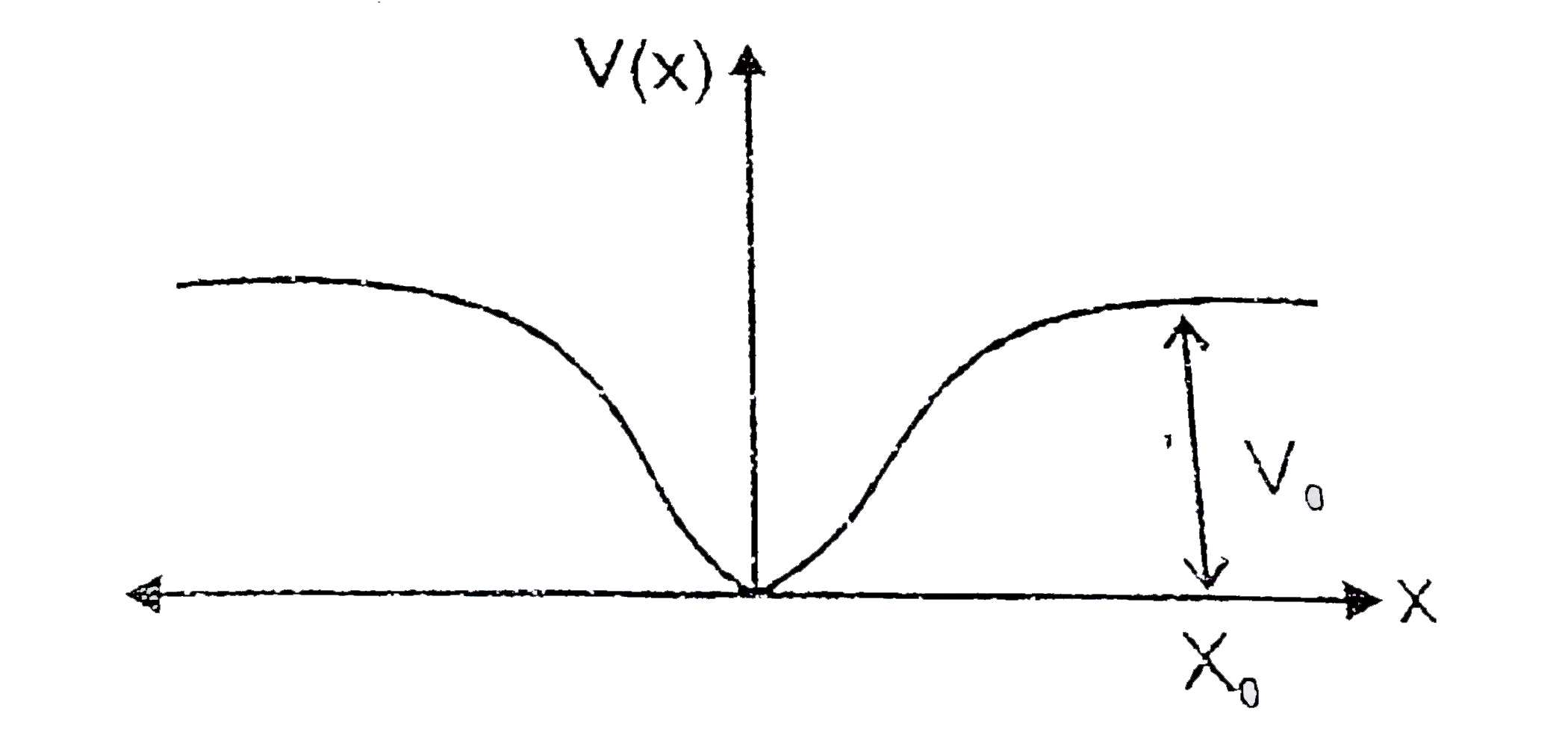
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MOTION-SIMPLE HARONIC MOTION -EXERCISE -4 (Leve-II) [ JEE 2011]
- When a particle is mass m moves on the x- axis in a potential of the f...
Text Solution
|
- When a particle is mass m moves on the x- axis in a potential of the f...
Text Solution
|
- When a particle is mass m moves on the x- axis in a potential of the f...
Text Solution
|
- A point mass is subjected to two simultaneous sinusoidal displacement...
Text Solution
|
- A small block is connected to one end of a massless spring of un-stret...
Text Solution
|
- Phase space diagrams are useful tools in analysing all kond of dynamic...
Text Solution
|
- Phase space diagrams are useful tools in analysing all kond of dynamic...
Text Solution
|
- Phase space diagrams are useful tools in analysing all kond of dynamic...
Text Solution
|
- A particle of mass m is attached to one end of a mass-less spring of f...
Text Solution
|
- Two independent harmonic oscillators of equal mass are oscillating abo...
Text Solution
|
- A block with mass (M) is connected by a massless spring with stiffness...
Text Solution
|