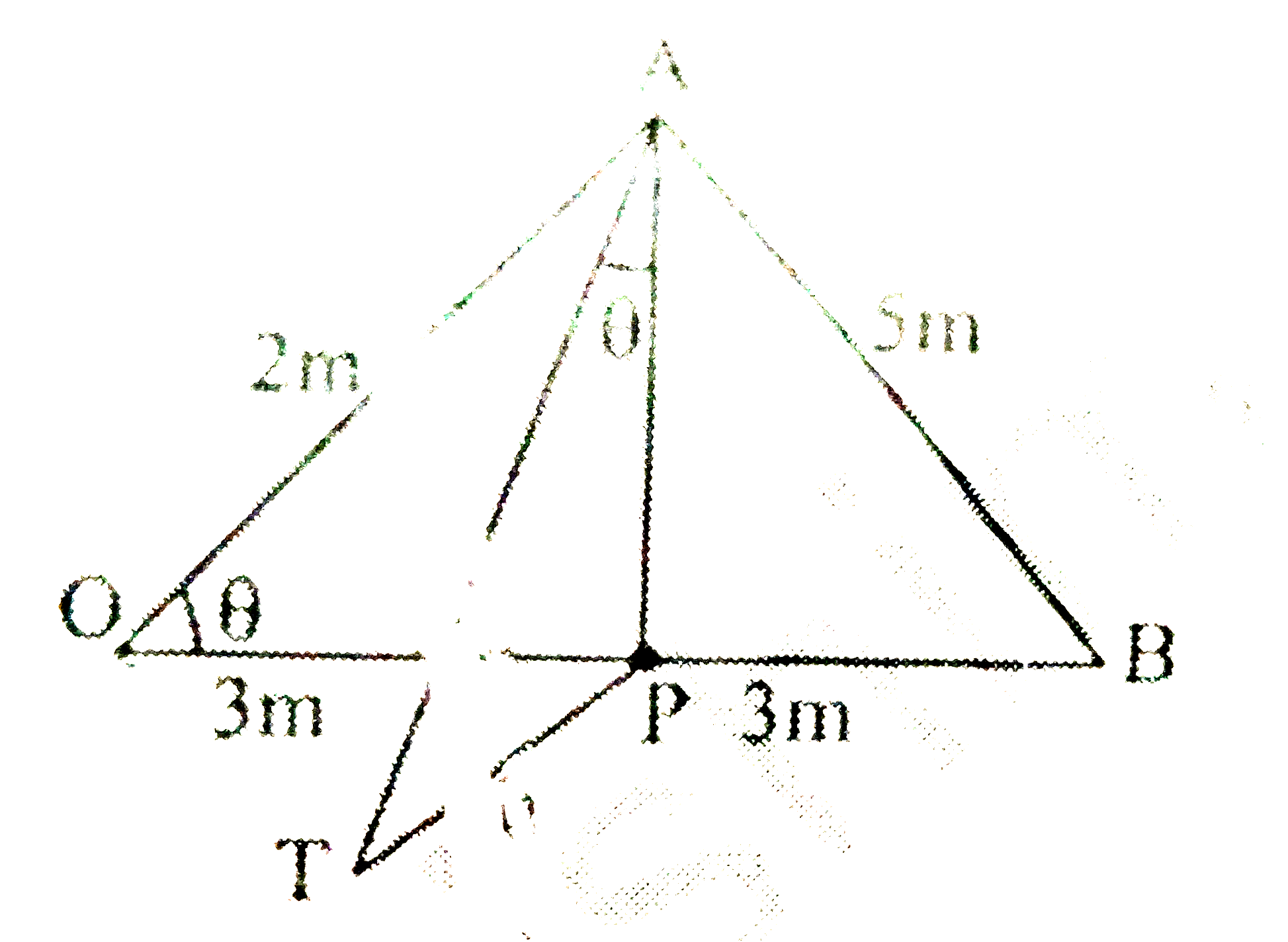Home
Class 12
MATHS
OAB is a triangle in the horizontal pla...

` OAB ` is a triangle in the horizontal plane through the foot ` P ` of the tower at the middle point of the side ` OB ` of the triangle. If ` OA = 2m, OB = 6 m, AB = 5 m and /_AOB ` is equal to the angle subtended by the tower at ` A,` then the height of the tower is

A

`sqrt((11xx39)/(25xx3))`

B

`sqrt((11xx39)/(25xx2))`

C

`sqrt((11xx25)/(39xx2))`

D

None of these

Text Solution

Verified by Experts

The correct Answer is:
2

`In Delta AOB`
`cos theta =(4+6-25)/(2xx6)=15/24=5/8`
`rArr 5/8 =(13-h^(2)xx25//39)/(12)`
`rArr h^(2) = 11/2xx39/25`
Promotional Banner

Topper's Solved these Questions

  • MOCK TEST 8

    CAREER POINT|Exercise PART (C ) - MATHS|30 Videos

Similar Questions

Explore conceptually related problems

OAB is a triangle in the horizontal plane through the foot P of the tower at the middle point of the side OB of the triangle.If OA=2m,OB=6m,AB=5m and /_AOB is equal to the angle subtended by the tower at A, then the height of the tower is

PQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to theta . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is . Then prove that the height of the tower is (abc) tantheta/(4)dot

At a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30^@ The height of the tower is

The angle of elevation of the top of a tower from two points A and B lying on the horizontal through the foot of the tower are respectively 15^(@)and30^(@) .If A and B are on the same side of the tower and AB = 48 metre , then the height of the tower is :

From the top of cliff 50 m high the angle fo elevation of a tower is found to be equal ot the angle of depression of the foot of the tower. The height of the tower is …….

A tower of height b subtends an angle at a point 0 on the ground level through the foot of the tower and at a distance a from the foot of the tower. A pole mounted on the top of the tower also subtends an equal angle at 0. The height of the pole is

CAREER POINT-MOCK TEST 9-MATHS
  1. OAB is a triangle in the horizontal plane through the foot P of the...

    Text Solution

    |

  2. If vec x and vec y are two non-collinear vectors and ABC is a triangle...

    Text Solution

    |

  3. If the volume of tetrahedron A B C D is 1 cubic units, where A(0,1,...

    Text Solution

    |

  4. The equation of the plane passing through the lines (x-4)/(1)=(y-3)/(1...

    Text Solution

    |

  5. The Delta with vertices (x(i),y(i)) i=1,2,3 "is inscribed in the circl...

    Text Solution

    |

  6. If the line px + qy =1 is a tangent to the parabola y^(2) =4ax, then

    Text Solution

    |

  7. If int (2tan x+3)/(sin^(2)x+2cos^(2)x)dx =1(n)(1+sec^(2)x)+ p tan^(-...

    Text Solution

    |

  8. If f'(x^2-4x+3)gt0 " for all " x in (2,3) then f(sinx) is increasing ...

    Text Solution

    |

  9. If f(x) is continuous and increasing functin such that the domain of g...

    Text Solution

    |

  10. If f(x)={alpha+sin[x]/x , x > 0 and 2 ,x=0 and beta+[(sin x-x)/x^3] ,x...

    Text Solution

    |

  11. Find the greatest value of the term independent of x in the expansion ...

    Text Solution

    |

  12. The polynomial f(x)=x^4+a x^3+b x^3+c x+d has real coefficients and f(...

    Text Solution

    |

  13. If b^(2) -ac lt 0 and a gt 0 then the value of the determinant is

    Text Solution

    |

  14. The probability that sin^(-1)(sin x)+cos^(-1)(cos y) is an integer x, ...

    Text Solution

    |

  15. If the points P(alpha,0) and Q(0,beta) always lies inside sthe Delta f...

    Text Solution

    |

  16. The equation of the hyperbola whose foci are (6.5), (-4,5) and eccentr...

    Text Solution

    |

  17. The value of the definite integral int(0)^(3pi//4)(1+x)sin x+(1-x) cos...

    Text Solution

    |

  18. The value of the constant 'm' and 'c' for which y = mx + c is a soluti...

    Text Solution

    |

  19. Through the centriod of an equilateral triangle a line parallel to the...

    Text Solution

    |

  20. If the number of ways of selecting 3 numbers out of 1, 2, 3, ……., 2n+1...

    Text Solution

    |