Home
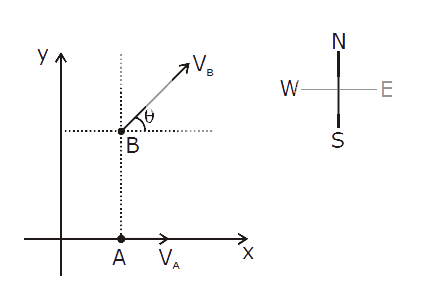
Class 12
PHYSICS
Figure shows two ships moving in x-y pla...

Figure shows two ships moving in x-y plane with velocity ` V_(A) " and "V_(B) ` . The ships move such that B always
remains north of A . The ratio ` (V_(A))/(V_(B))` is eqal to -

A

` cos theta `

B

`sin theta `

C

`sec theta `

D

` " cosec" theta `

Text Solution

Verified by Experts

The correct Answer is:
A
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • ONE DIMENSION MOTION

    MOTION|Exercise Exercise - 3 | Section - A Previous Year Problems | NEET|25 Videos

  • ONE DIMENSION MOTION

    MOTION|Exercise Exercise - 3 |Section - B Previous Year Problems | JEE MAIN|12 Videos

  • ONE DIMENSION MOTION

    MOTION|Exercise EXERCSE -2 (Section - E : River Boat Problems)|3 Videos

  • NLM & FRICTION

    MOTION|Exercise EXERCISE-4 ( LEVEL-II)|15 Videos

  • OPTICS

    MOTION|Exercise Exercise|45 Videos

Similar Questions

Explore conceptually related problems

In the circuit shown in the figure, the ratio of V_(B) as V_(C) is

In the system shown, the block A is moving down eith velocity v_(1) and C is moving up with velocity v_(3) . Express velocity of the block B in terms of velocities of the blocks a and C.

Knowledge Check

  • The displacement - time graph for two particles A and B is as follows. The ratio (v_(A))/(v_(B)) is

    A
    `1:2`
    B
    `1:sqrt3`
    C
    `sqrt3:1`
    D
    `1:3`

  • If block A is moving horizontally with velocity v_(A) , then find the velocity of block B at the instant as shown in fig.

    A
    `(hv_(A))/(2sqrt(x^(2)+h^(2)))`
    B
    `(xv_(A))/(sqrt(x^(2)+h^(2)))`
    C
    `(xv_(A))/(2sqrt(x^(2)+h^(2)))`
    D
    `(hv_(A))/(sqrt(x^(2)+h^(2)))`

  • Two objects A and B are moving in opposite directions with velocities v_(A) and v_(B) respectively, the magnitude of relative velocity of A w.r.t. B is

    A
    `v_(A)-v_(B)`
    B
    `v_(A)+v_(B)`
    C
    `v_(B)-v_(A)`
    D
    `v_(A)//v_(B)`

    • Similar Questions

    Explore conceptually related problems

    A particle of mass m is moving with constant velocity v_(0) along the line y=b . At time t=0 it was at the point (0,b) . At time t=(b)/(v_(0)) , the

    In fig., blocks A and B move with velocities v_(1) and v_(2) along horizontal direction. Find the ratio of v_(1)//v_(2)

    Two particles of mass m_(A) and m_(B) and their velocities are V_(A) and V_(B) respectively collides. After collision they interchanges their velocities, then ratio of m_(A)/m_(B) is

    A sphere A of mass m moving with a velocity hits another stationary sphere B of same mass. If the ratio of the velocity of the sphere after collision is (v_(A))/(v_(B)) = (1 - e)/(1 + e) where e is the cofficient of restitution, what is the initial velocity of sphere A with which it strikes?

    Two planets A and B have the same material density. If the radius of A is twice that of B , then the ratio of the escape velocity (v_(A))/(v_(B)) is

    Home
    Profile