Home
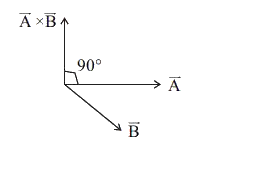
Class 11
PHYSICS
If the angle between the vectors vecA an...

If the angle between the vectors `vecA and vecB` is `theta,` the value of the product `(vecB xx vecA) * vecA` is equal to

A

`BA^(2) cos theta`

B

`BA^(2) sin theta `

C

`BA^(2) sin theta cos theta `

D

Zero

Text Solution

Verified by Experts

The correct Answer is:
D
Angle between `vecB xx vecA and vecA ` is `90^(@)`
`(vecB xx vecA). vecA=|vecB xx vecA||vecA| cos 90^(@)`
`=0`
Promotional Banner

Topper's Solved these Questions

  • KINEMATICS

    CBSE COMPLEMENTARY MATERIAL|Exercise Numericals|26 Videos

  • GRAVITATION

    CBSE COMPLEMENTARY MATERIAL|Exercise MULTIPLE CHOICE QUESTIONS|19 Videos

  • KINETIC THEORY OF GASES

    CBSE COMPLEMENTARY MATERIAL|Exercise Objective question|20 Videos

Similar Questions

Explore conceptually related problems

The angle between the vector vecA and vecB is theta . The value of the triple product vecA.(vecBxxvecA) is

The angle between vector (vecA) and (vecA-vecB) is :

The angle between vectors (vecA xx vecB) and (vecB xx vecA) is :

If veca, vecb and vecc are three vectors, such that |veca|=2, |vecb|=3, |vecc|=4, veca. vecc=0, veca. vecb=0 and the angle between vecb and vecc is (pi)/(3) , then the value of |veca xx (2vecb - 3 vecc)| is equal to

If the vectors veca and vecb are mutually perpendicular, then veca xx {veca xx {veca xx {veca xx vecb}} is equal to:

If theta is the angle between unit vectors vecA and vecB , then ((1-vecA.vecB))/(1+vecA.vecB)) is equal to

The value of the sum of two vectors vecA and vecB with theta as the angle between them is

Assertion: If theta be the angle between vecA and vecB then tan theta=(vecAxxvecB)/(vecA.vecB) Reason: vecAxxvecB is perpendicular to vecA.vecB

If veca , vecb and vecc are non- coplanar vectors and veca xx vecc is perpendicular to veca xx (vecb xx vecc) , then the value of [ veca xx ( vecb xx vecc)] xx vecc is equal to

Let veca and vecb be two non-zero vectors perpendicular to each other and |veca|=|vecb| . If |veca xx vecb|=|veca| , then the angle between the vectors (veca +vecb+(veca xx vecb)) and veca is equal to :

CBSE COMPLEMENTARY MATERIAL-KINEMATICS-M.C.Q.
  1. If the angle between the vectors vecA and vecB is theta, the value of ...

    Text Solution

    |

  2. For an object thrown at 45^(@) to the horizontal, the maximum height H...

    Text Solution

    |

  3. the circular motion of a particle with constant speed is

    Text Solution

    |

  4. At the uppermost point of a projectile, its velocity and acceleration ...

    Text Solution

    |

  5. If |vecA + vecB| = |vecA - vecB|, then the angle between vecA and vecB...

    Text Solution

    |

  6. The x and y coordinates of a particle at any time t is given by x = 7t...

    Text Solution

    |

  7. If K is the kinetic energy of a projectile fired at an angle 45°, then...

    Text Solution

    |

  8. A particle is moving eastwards with a velocity of 5 m//s. In 10 s the...

    Text Solution

    |

  9. A body dropped from top of tower falls through 60 m during the last 2 ...

    Text Solution

    |

  10. The angular velocity of second's hand of a watch will be.

    Text Solution

    |

  11. the angle between the vectors (hati+hatj) and (hatj+hatk) is

    Text Solution

    |

  12. If the scalar and vector products of two vectors vecA and vecB are equ...

    Text Solution

    |

  13. An object , moving with a speed of 6.25 m//s , is decelerated at a ra...

    Text Solution

    |

  14. The velocity time graph for the veticaly component of the velocity of ...

    Text Solution

    |

  15. In one second, a particle goes from point A to point B moving in a sem...

    Text Solution

    |

  16. A boat which has a speed of 5 km per hour in still water crosses a riv...

    Text Solution

    |

  17. A body projected at an angle with the horizontal has a range 300 m. th...

    Text Solution

    |

  18. What is the projection of vecA on vecB ?

    Text Solution

    |

  19. A person travels along a straight road for the first half length with ...

    Text Solution

    |

  20. A projectile rises to a height of 10 m and then falls at a distance of...

    Text Solution

    |