Home
Class 9
MATHS
In figure, P is the mid-point of side BC...

In figure, P is the mid-point of side BC of a parallelogram ABCD such that `angleBAP=angleDAP`. Prove that AD = 2CD. ltBrgt

Text Solution

Verified by Experts

The correct Answer is:
Prove
Promotional Banner

Topper's Solved these Questions

  • QUARILATERAL

    CBSE COMPLEMENTARY MATERIAL|Exercise Part - D|5 Videos

  • QUARILATERAL

    CBSE COMPLEMENTARY MATERIAL|Exercise Part - B|12 Videos

  • PROBABILITY MIND MAP

    CBSE COMPLEMENTARY MATERIAL|Exercise PRACTICE TEST|6 Videos

  • STATISTICS

    CBSE COMPLEMENTARY MATERIAL|Exercise PRACTICE TEST|5 Videos

Similar Questions

Explore conceptually related problems

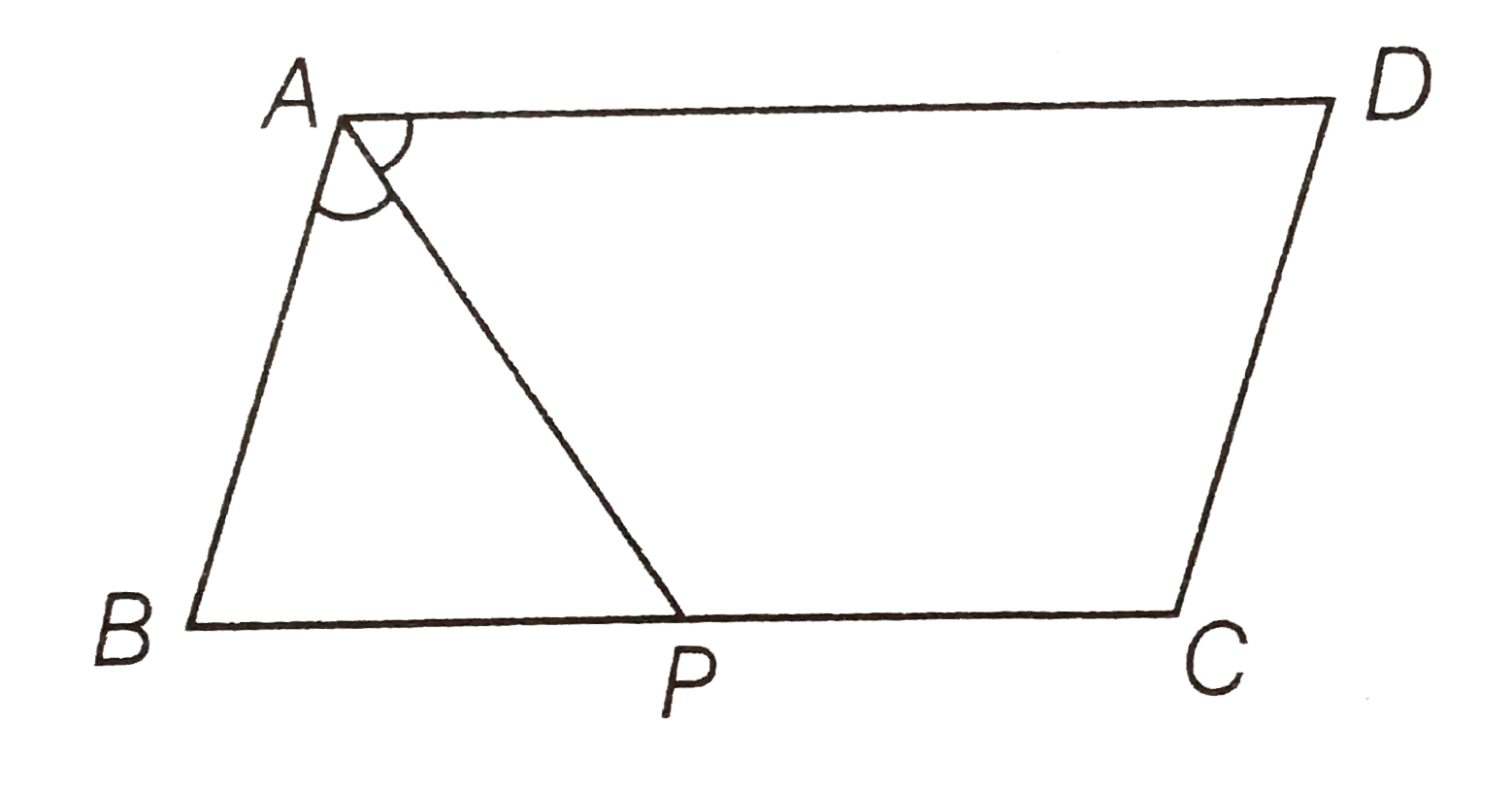
In the given figure, P is the mid-point of side BC of a parallelogram ABCD such that angleBAP=angleDAP. Prove that AD = 2CD.

The mid-point of side CD of parallelogram ABCD is 'm' in the given figure what is the ratio ON : OB?

If D is the mid-point of the side BC of a triangle ABC, prove that vec AB+vec AC=2vec AD .

E and F are the mid-points of the sides AB and CD of a parallelogram ABCD. Prove that the line segment AF and CE trisects BD in three equal parts.

P is the mid-point of side AB of a parallelogram ABCD .A Line through B parallel to PD meets DC at Q and AD produced at R. Prove that ( i )AR=2BC (ii) BR=2BQ.

If E is a point on side AD produced of a parallelogram ABCD and BE intersects CD at F . Prove that DABE^(-)DCFB

If P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to

P is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that : (i) AR = 2BC (ii) BR= 2BQ