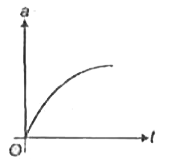
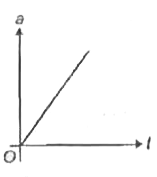
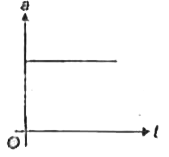
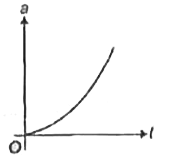
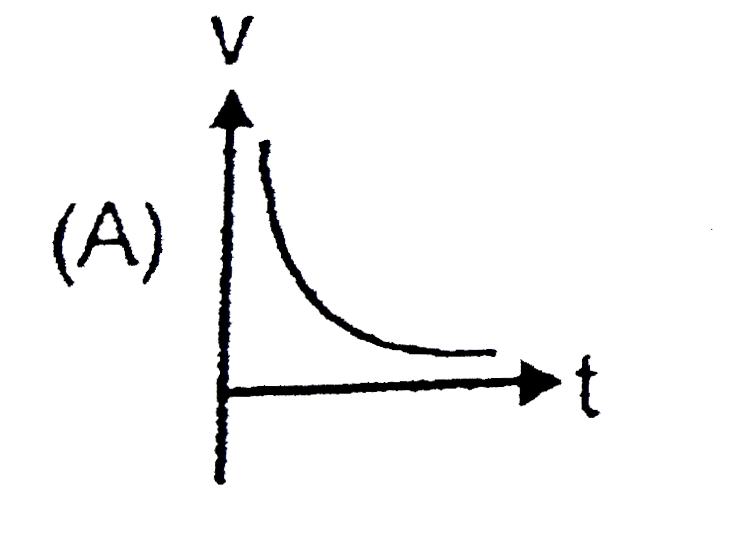
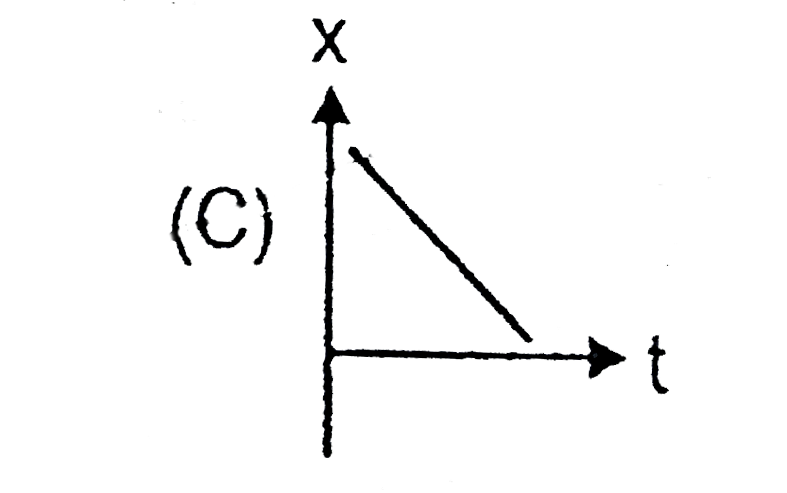
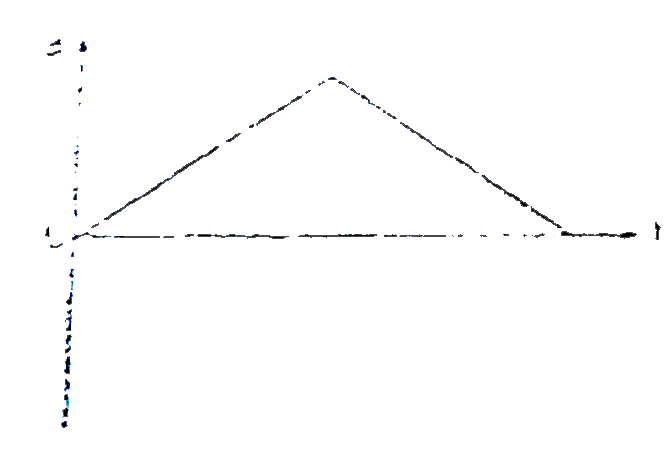
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
MOTION IN A STRAIGHT LINE
AAKASH INSTITUTE|Exercise ASSIGNMENT (SECTION - C)|37 VideosView PlaylistMOTION IN A STRAIGHT LINE
AAKASH INSTITUTE|Exercise ASSIGNMENT (SECTION - D)|15 VideosView PlaylistMOTION IN A STRAIGHT LINE
AAKASH INSTITUTE|Exercise ASSIGNMENT (SECTION - A)|60 VideosView PlaylistMOTION IN A PLANE
AAKASH INSTITUTE|Exercise Assignement section -J (Aakash Challengers Questions)|4 VideosView PlaylistMOTION IN STRAIGHT LINE
AAKASH INSTITUTE|Exercise Assignment (SECTION - J)|2 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE-MOTION IN A STRAIGHT LINE-ASSIGNMENT (SECTION - B)
- The velocity v of a body moving along a straight line varies with time...
02:31
|
Play - The relation between position (x) and time (t) are given below for a p...
05:25
|
Play - The velocity v of a particle moving along x - axis varies with ist pos...
02:19
|
Playing Now - The velocity (upsilon) of a particle moving along X-axis varies with i...
02:26
|
Play - A ball is dropped from an elevator moving upward with acceleration 'a'...
01:55
|
Play - The velocity (v) - time (t) graph for a particle moving along x - axis...
03:23
|
Play - The speed - time graph for a body moving along a straight line is show...
02:44
|
Play - The acceleration (a)-time(t) graph for a particle moving along a strai...
02:43
|
Play - A ball is thrown upward with speed 10 m/s from the top to the tower re...
02:18
|
Play - A ball dropped from the top of tower falls first half height of tower ...
02:38
|
Play - An object thrown verticallly up from the ground passes the height 5 m ...
04:23
|
Play - A particle is thrown vertically upwards. If its velocity is half of th...
02:11
|
Play - A particle starts with initial speed u and retardation a to come to re...
06:56
|
Play - Which of the following speed - time (v - t) graphs is physically not p...
01:53
|
Play - A particle travels half the distance of a straight journey with a spee...
05:33
|
Play - The acceleration - time graph for a particle moving along x - axis is ...
02:31
|
Play - A body falling a vertically up with initial velocity 52 m/s from the g...
04:07
|
Play - A body falling from a vertical height of 10 m pierces through a distan...
02:17
|
Play - When a particle is thrown vertically upwards, its velocity at one thir...
03:57
|
Play - A body is dropped from a height H. The time taken to cover second half...
02:08
|
Play