A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT FINGERTIPS-GRAVITATION-Energy Of An Orbiting Satellite
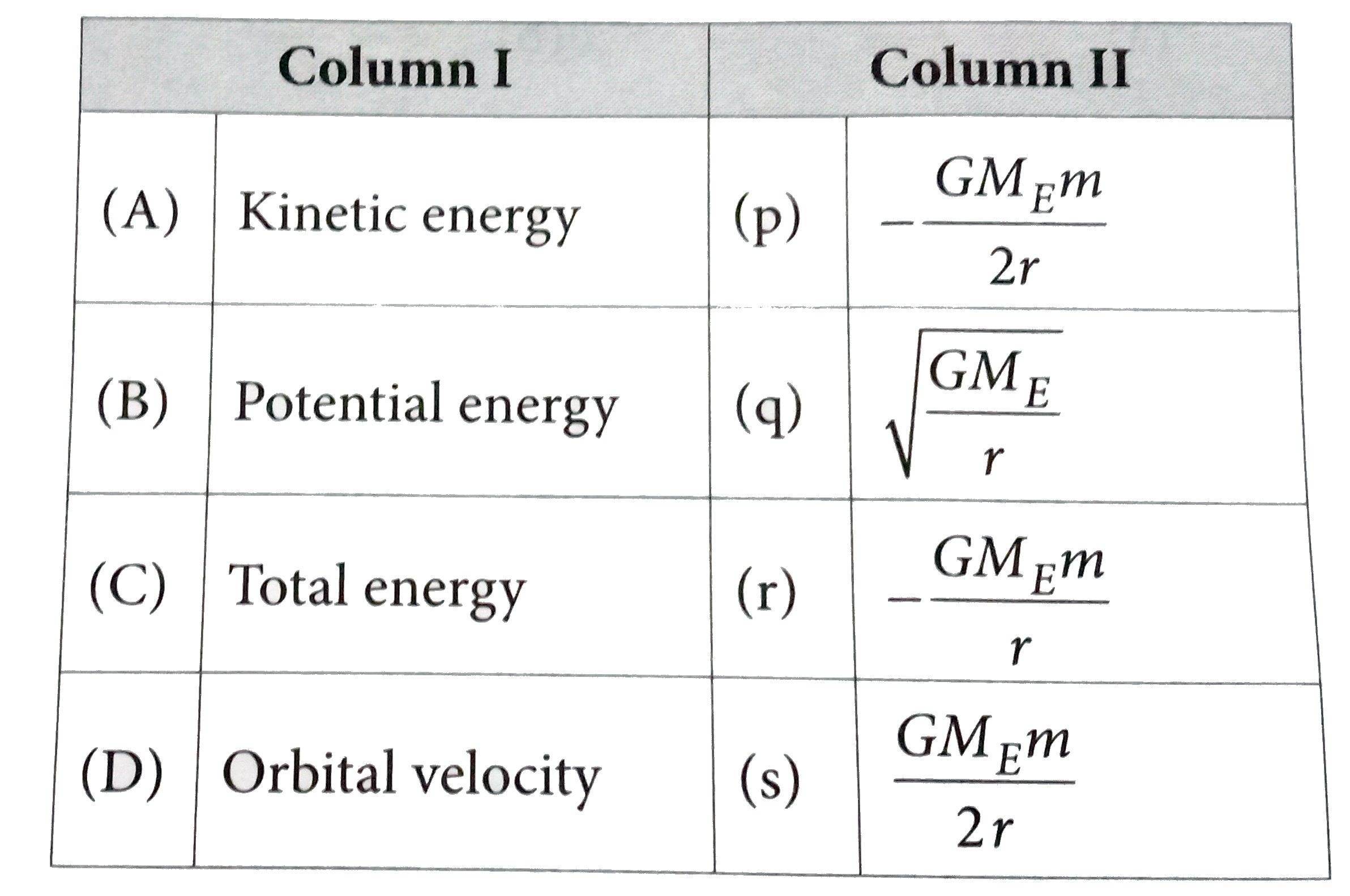
- Match the Column I with Column II For a satellite in circular orbit ...
Text Solution
|
- A satellite is orbiting the earth in a circular orbit of radius r. Its
Text Solution
|
- The figure shows the variation of energy with the orbit radius of a bo...
Text Solution
|
- Two satellites of earth S(1) and S(2) are moving in the same orbit. Th...
Text Solution
|
- In motion of an object under the gravitational influence of another ob...
Text Solution
|
- A comet orbits the Sun in a highly elliptical orbit. Does the comet ha...
Text Solution
|
- A satellite of mass m is in a circular orbit of radius 2R(E) about the...
Text Solution
|
- in the previous question, the change in potential energy.
Text Solution
|
- The additional kinetic energy to be provided to a satellite of mass m ...
Text Solution
|
- A satellite of a mass m orbits the earth at a height h above the surfa...
Text Solution
|
- For a satellite moving in a circular orbit around the earth, the ratio...
Text Solution
|
- An artificial satellite moving in a circular orbit around the earth ha...
Text Solution
|
- A rocket is launched vertically from the surface of earth with an init...
Text Solution
|
- An asteroid of mass m is approaching earth, initially at a distance 10...
Text Solution
|
- Two stars each of mass M and radius R are approaching each other for a...
Text Solution
|