Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT-PAIR OF LINEAR EQUATIONS IN TWO VARIABLES-EXERCISE 3.7
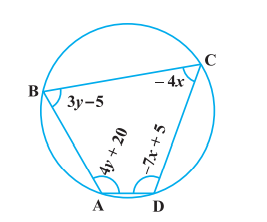
- ABCD is a cyclic quadrilateral (see Figure). Find the angles of the c...
Text Solution
|
- In a DeltaA B C ,/C=3 /B=2(/A+/B). Find the three angles.
Text Solution
|
- The students of a class are made to stand in rows. If 3 students are ...
Text Solution
|
- Solve the following pair of linear equations: (i) p x+q y=p q ;\ q ...
Text Solution
|
- Draw the graphs of the equations 5x y=5and 3x y=3. Determine the co...
Text Solution
|
- The ages of two friends Ani aid Biju differ by 3 years. Ani's father ...
Text Solution
|
- A train covered a certain distance at a uniform speed. If the train w...
Text Solution
|
- One says, if you give me a hundred, friend ! I shall then become twic...
Text Solution
|