A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
TEST PAPER
ALLEN|Exercise PHYSICS SECTION-II|8 VideosView PlaylistTEST PAPER
ALLEN|Exercise CHEMISTRY SECTION-I|10 VideosView PlaylistTEST PAPER
ALLEN|Exercise MATHEMATICS|20 VideosView PlaylistSEQUENCE AND PROGRESSION
ALLEN|Exercise Exercise (JA)|12 VideosView PlaylistTEST PAPERS
ALLEN|Exercise CHEMISTRY|1 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
ALLEN-TEST PAPER-PHYSICS SECTION-I
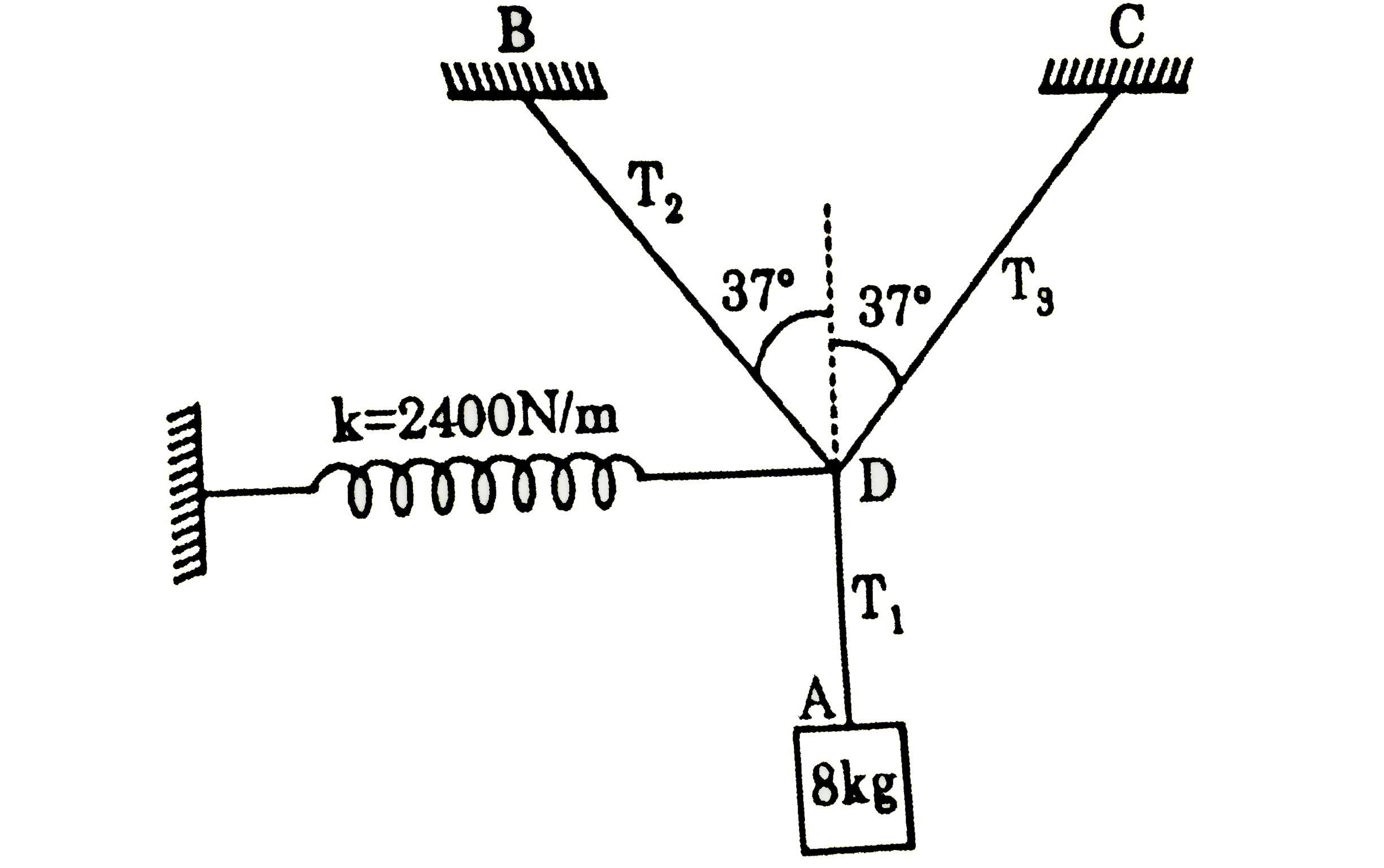
- Given arrangement is in equilibrium and elongation in spring is 1cm. T...
Text Solution
|
Playing Now - Net force acting on a particle is always perpendicular to its velocity...
Text Solution
|
Play - Two blocks on horizontal ground are connected by a spring. At an insta...
Text Solution
|
Play - A bead is moving on a frictionless fixed circular wire of radius 0.8 m...
Text Solution
|
Play - Choose the CORRECT statements
Text Solution
|
Play - A particle stays at rest as seen in frame. Then which of the following...
Text Solution
|
Play - In the List-I some arrangement with ideal string & frictionless & ligh...
Text Solution
|
Play - Figure shows a practical situation.The event is observed by four obser...
Text Solution
|
Play - In the given figure
Text Solution
|
Play - Study the velocity-time graph pictured below and match each segment of...
Text Solution
|
Play