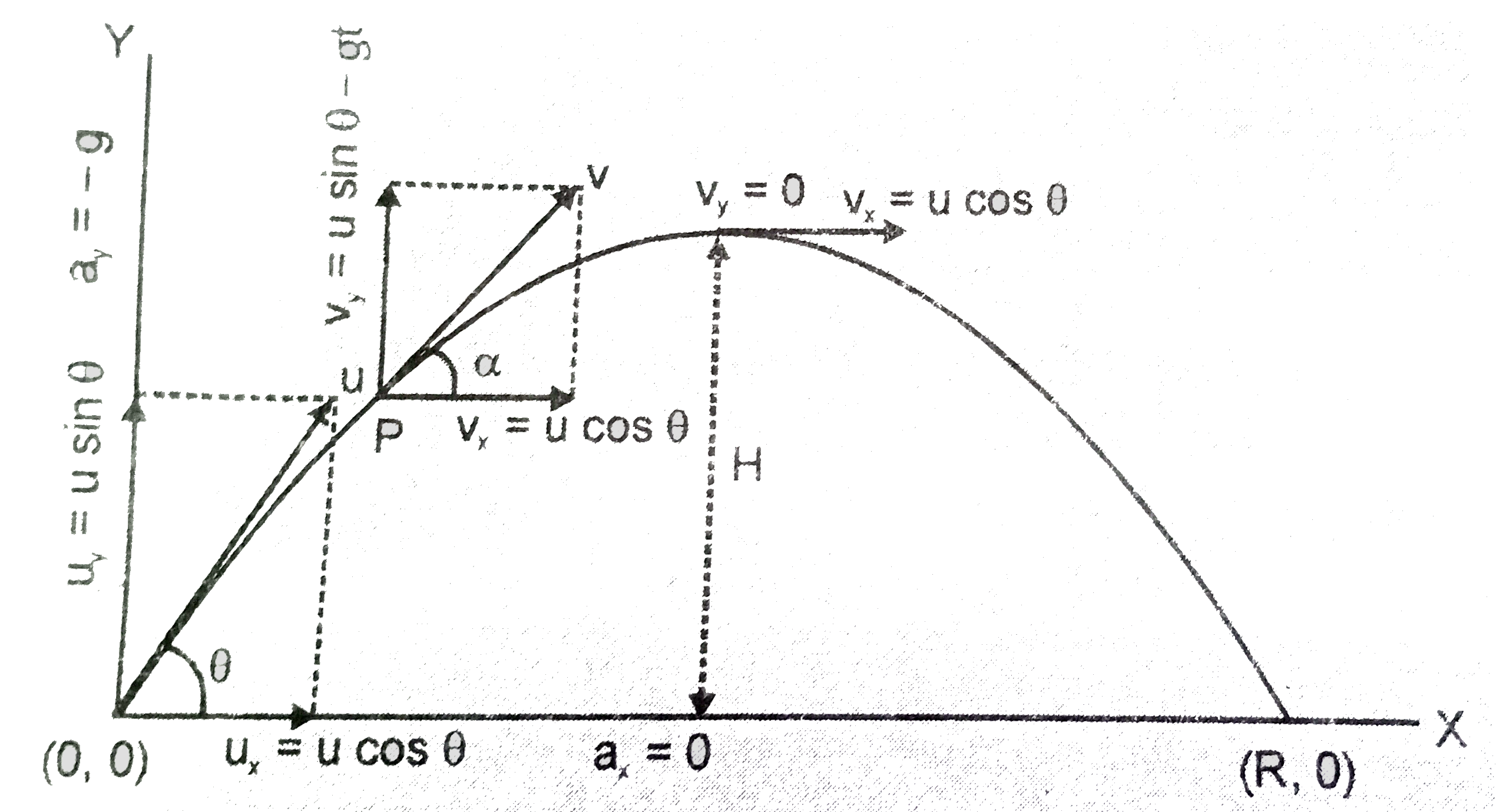Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-MOTION IN A PALNE-SOLVED EXAMPLE
- A particle thrown over a triangle from one end of a horizontal base fa...
Text Solution
|
- A projectile is fired horizontally with a velocity of 98 ms^(-1) from ...
Text Solution
|
- Two tall buildings face each other and are at a distance of 180 m from...
Text Solution
|
- Two paper screens A and B are separated by a distance of 100m. A bulle...
Text Solution
|
- A ball rolls off top of a stair case with horizontal velocity u (m)/(s...
Text Solution
|
- A football player kicks a ball at ball at an angle of 30 ^(0) with the...
Text Solution
|
- A cricketer can throw a ball to a maximum horizontal distance of 100 m...
Text Solution
|
- A ball is thown at angle theta and another ball is thrown at angle (90...
Text Solution
|
- Two bodies are thrown with the same initial speed at angles alpha and ...
Text Solution
|
- The range of a projectile launched at an angle of 15^(@) with horizont...
Text Solution
|
- A ball of mass (m) is thrown vertically up. Another ball of mass 2 m ...
Text Solution
|
- A body is projectd with the velcity (U1) from the point (A) as shown...
Text Solution
|
- An aeroplane is flying at a constant height of 1960 m with speed 600 k...
Text Solution
|
- A body is projected up such that its position vector varies with time ...
Text Solution
|
- Two particles A and B are projected simultaneously in the directins sh...
Text Solution
|
- Two bodies were thrown simultaneously from the same point, one straigh...
Text Solution
|
- Two particles are projected from the two towers simultaneously, as sho...
Text Solution
|
- A projectile is thrown with speed u making angle theta with horizontal...
Text Solution
|
- A particle has an initial velocity (6hati+8hatj) ms^(-1) and an accele...
Text Solution
|
- A particle travels according to the equation y=x-(x^(2)/(2)). Find the...
Text Solution
|