Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT-TRIANGLES-EXERCISE 7.4
- In Fig. 7.49, /B\ < /A and /C\ < /D. Show that A D\ < \ B C.</b>
Text Solution
|
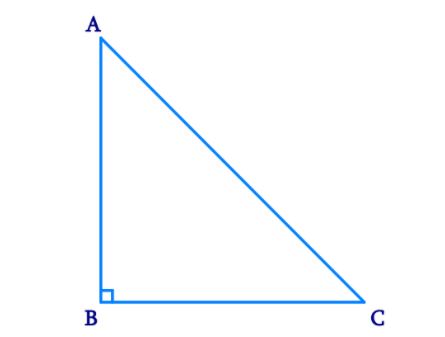
- Show that in a right angled triangle, the hypotenuse is the longest s...
Text Solution
|
- AB and CD are respectively the smallest and longest sides of a quadril...
Text Solution
|
- Show that of all line segments drawn from a given point not on it, th...
Text Solution
|
- In Fig. 7.48, sides AB and AC of DeltaA B C are extended to points P ...
Text Solution
|
- In Fig 7.51, P R\ >\ P Qand PS bisects /Q P R. Prove that /P S R\ >/P...
Text Solution
|