The given quantity of metal is to be cost into a half cylinder with a rectangular base and semicircular ends. Show that in order that the total surface area may be minimum, the ratio of the length of the cylinder to the diameter of its semi-circular ends is `pi:(pi+2)dot`

Explanation

Let r be the radius and the h be the height of half cylinder
Volume `=(1)/(2) pir^(2)h = V` (Constant )…………….(1)

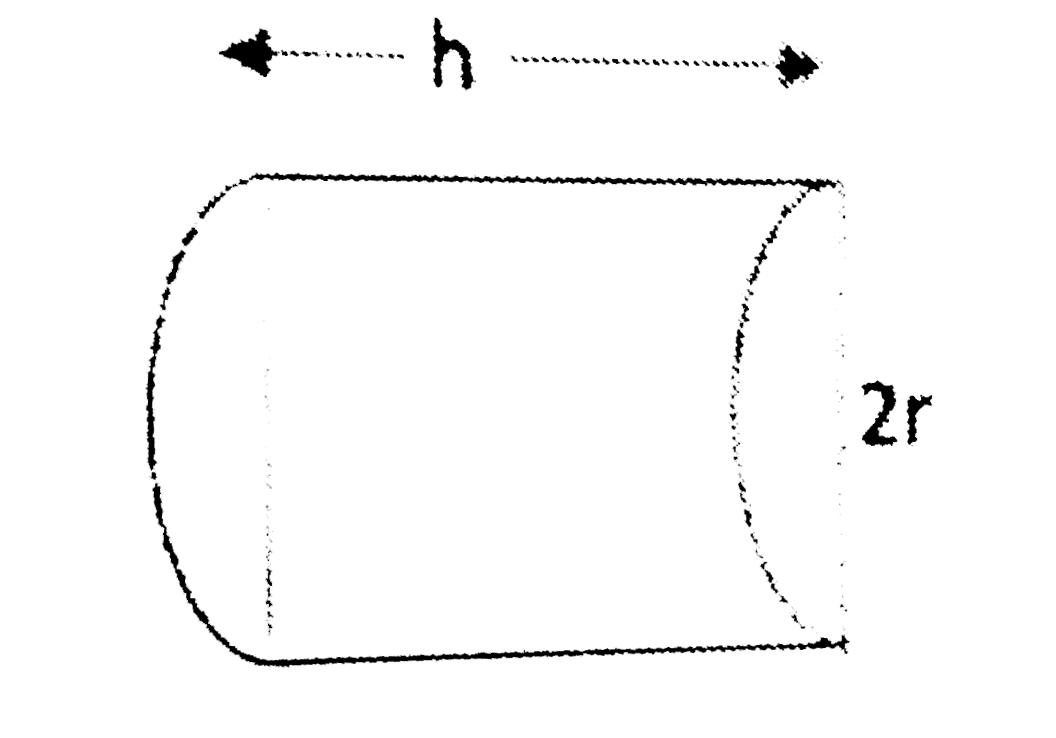
Total surface area of half cylinder is
`S=2(1/2pir^(2))+pirh+2rh……….(2)`
from (1) put the value of h in (2)
`S=(pir^(2))+pir((2V)/(pir^(2)))+2r((2V)/(pir^(2)))`
`S=(pir^(2))+(1/r)[(4V)/pi+2V]`
`(ds)/(dr)=(2pir)+((-1)/r^(2))[(4V)/pi+2V]....(3)`
For maxima/minima`(ds)/(dr)`=0
`rArr(2pir)+((-1)/r^(2))[(4V)/pi+2V]=0`
`rArr(2pir)=(1/r^(2))[(4V+2Vpi)/pi]`
`rArrpir^(3)=V[(2+pi)/pi)]`
`rArrV=(pi^(2)r^(3))/(pi+2)..........(4)`
From (1) and (4)
`rArr1/2pir^(2)h=(pi^(2)r^(3))/(pi+2)`
`rArrh/(2r)=pi/(pi+2)`
`rArr` height : diameter `=pi:pi+2`
Differentiating (3) with respect to r
`(d^(2)s)/(dr(2))=(2pi)+(2)/(r^(3))[(4V)/pi+2V]`= positive (as all quantities are +ve)
So, S is minimum when
height: diameter=`pi:pi+2`