Text Solution
Verified by Experts
Topper's Solved these Questions
FULL MARKS-SURFACE CHEMISTRY-ADDITIONAL QUESTIONS (5 Marks questions)
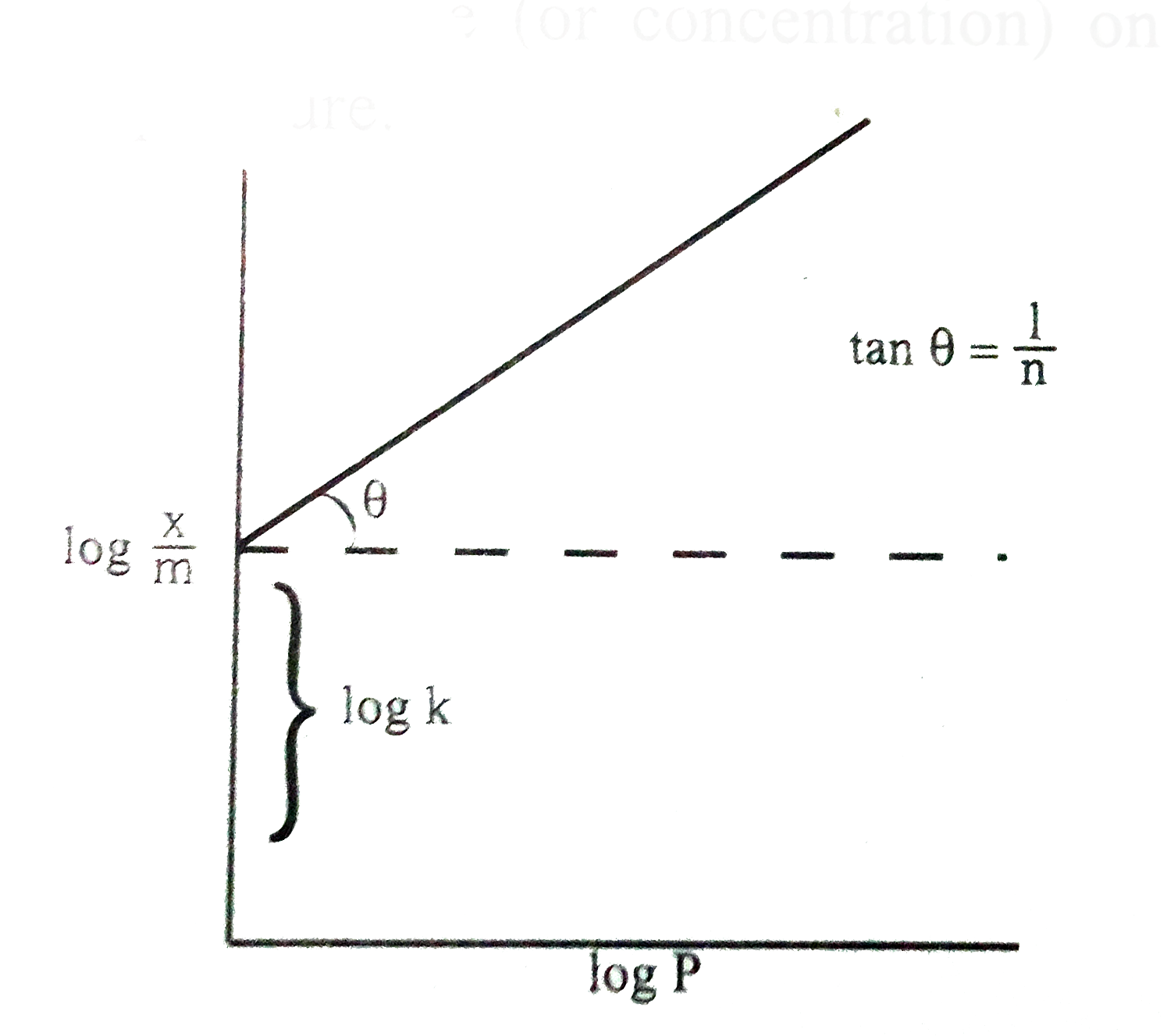
- What is adsorption isotherm? Explain about Freundlich adsorption isoth...
Text Solution
|
- Define catalyst. What are the characteristics of catalysts?
Text Solution
|
- What is enzyme catalysis? Give the characteristics of enzyme catalysed...
Text Solution
|
- Explain about phase transfer catalysis.
Text Solution
|
- Explain about the classification of colloids based on the physical sta...
Text Solution
|
- Describe about condensation methods of preparation of colloids. (OR) D...
Text Solution
|
- Describe about the properties of colloids.
Text Solution
|
- Explain about Electrophoresis (or) Cataphoresis (or) How would you det...
Text Solution
|
- What are emulsion? Mention its type with example. What is emulsificati...
Text Solution
|
- What is deemulsification? Explain about the various techniques of deem...
Text Solution
|
- (a) How can a colloidal solution and a true solution of the same colou...
Text Solution
|
- Illustrate with examples - (i) Lyophilic and Lyophobic sols (ii) H...
Text Solution
|