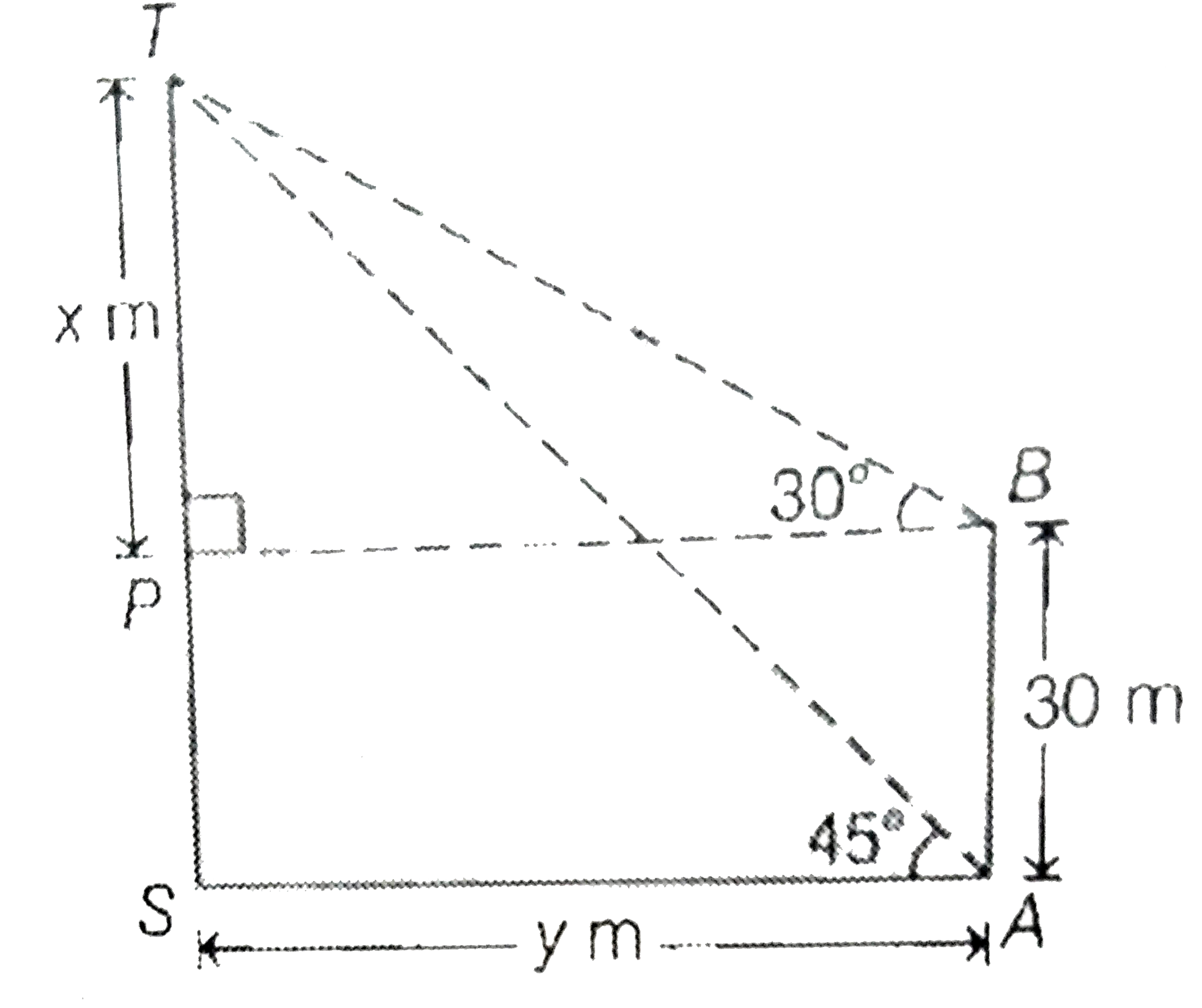
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
TRIGONOMETRICAL RATIOS AND IDENTITIES
IIT JEE PREVIOUS YEAR|Exercise MAXIMA AND MINIMA|4 VideosTRIGONOMETRICAL EQUATIONS
IIT JEE PREVIOUS YEAR|Exercise TOPIC 3 PROBLEMS BASED ON MAXIMUM AND MINIMUM OBJECTEIVE QUESTIONS I (ONLY ONE CORRECT OPTION)|9 VideosVECTOR ALGEBRA
IIT JEE PREVIOUS YEAR|Exercise Solving Equations and Reciprocal of Vectors (Objective Questions II) (Analytical & Descriptive Questions|8 Videos
Similar Questions
Explore conceptually related problems
IIT JEE PREVIOUS YEAR-TRIGONOMETRICAL RATIOS AND IDENTITIES-HEIGHT AND DISTANCE
- The angle of elevation of the top of a vertical tower standing on a ho...
Text Solution
|
- A 2 m ladder leans against a vertical wall. If the top of the ladder b...
Text Solution
|
- ABC is a triangular park with AB = AC = 100 m. A vertical tower is sit...
Text Solution
|
- Two poles standing on a horizontal ground are of heights 5 m and 10 m,...
Text Solution
|
- Two vertical poles of heights, 20 m and 80 m stand apart on a horizont...
Text Solution
|
- If the angle of elevation of a cloud from a point P which is 25 m abov...
Text Solution
|
- Consider a triangular plot ABC with sides AB = 7 m, BC = 5 m and CA =...
Text Solution
|
- PQR is a triangular park with PQ=PR=200m . A T.V tower stands at the m...
Text Solution
|
- Let a vertical tower AB have its end A on the level ground. Let C be t...
Text Solution
|
- A man is walking towards a vertical pillar in a straight path, at a ...
Text Solution
|