विद्युत द्विध्रुव के कारण किसी बिन्दु पर विद्युतीय विभव का व्यंजक - मान लिया कि AB एक विद्युतीय - द्विध्रुव है जिसके विजातीय आवेश +Q तथा -Q एक दूसरे से अल्पदूरी 2I पर स्थित है। द्विध्रुव के कारण किसी बिन्दु P पर विद्युत विभव का मान ज्ञात करना है । जिसके ध्रुवीय केंद्र O के सापेक्ष `(r,theta)` है , अर्थात OP= r तथा `angle POA= theta` बिन्दु A से PO पर खींचा गया लंब AN है इसी प्रकार बिन्दु B से बड़ी गयी रेखा PO पर खींचा गया लंब BM है , जैसा कि नीचे चित्र में दिखाया गया है।
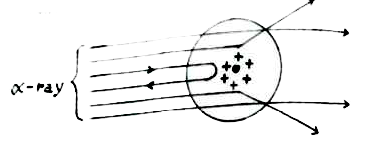
अब समकोण `Delta AON` में `ON=OA cos theta = l cos theta`
और समकोण `Delta BOM` में, `OM=OB cos theta= l cos theta`
अब चूँकि दोनों आवेगों के बीच की दूरी 2l बहुत कम है इसलिए PA लगभग PN के तथा PB लगभग PM बराबर होंगें । अतः `PA = PN=PO-ON= r-l cos theta`
और `PB=PM=PO+OM= r+l cos theta`
A पर स्थित +Q आवेग के कारण P बिन्दु पर विभव `V_(1) =+(1)/(4epsilon_(0))(Q)/(PA)=+(1)/(4piepsilon_(0))(Q)/((r-lcos theta))`
तथा B पर स्थित Q आवेग के कारण P बिन्दु पर विभव
`1=(1)/(4piepsilon_0)(Q)/(PB)=-(1)/(4piepsilon_0)(Q)/((r-lcos theta))`
P पर द्विध्रुव के कारण परिणाम विभव
`V=V_(1)+V_(2)=(Q)/(4piepsilon_0)[(1)/(r-lcos theta)-(1)/((r+lcos theta))]=(Q)/(4piepsilon_0)[(r+lcos -r +l cos theta)/((r^(2)-l^(2)cos theta))]=(Q)/(4piepsilon_0)(2lcos theta)/((r^(2)-l^(2)cos^(2)theta))=(1)/(4piepsilon_0)(P cos theta)/((r^(2)-l^(2)cos^(2)theta))`...(i)
जहाँ `P=theta xx 2l`, द्विध्रुव का आघूर्ण है फिर चूँकि `r^(2)` की तुलना में `l^(2) cos^(2) theta` का मान साम्य है। इसलिए समी (i) से P पर विभव
`V=(1)/(4piepsilon_0)(Pcos theta)/(r^2)`
यदि `hat( r).OP` की दिशा में एकांक सदिश हो तो
`vec (P). hat( r) = P xx l cos theta=P cos theta`
अतः समी (ii) को सदिश संकेत में हम इस प्रकार व्यक्त कर सकते है।
`V=(1)/(4piepsilon_0).(vec(P).hat( r))/( r^2)`.
कलन विधि द्वारा विद्युत क्षेत्र का परिकलन निम्न है - माना AB एक विद्युतीय - द्विध्रुव है। जिसके आवेग +Q तथा -Q के बीच की दूरी 2I है इसके मध्यबिन्दु O से r दूरी पर कोई बिन्दु P है। जहाँ विद्युत क्षेत्र की तीव्रता का मान निकालना है।
अगर बिन्दु P पर विद्युतीय विभव का मान v है तो `V=(1)/(4piepsilon_0).(Pcos theta)/(r^2)`
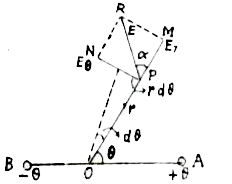
चित्र में स्पष्ट है कि OP दिशा में दूरी का परिवर्तन dr तथा उसके लंबवत PN दिशा में कोई परिवर्तन rd `theta` है। अब `Er = (dr)/(dr)=(d)/(dt)[(1)/(4piepsilon_0)(Pcos theta)/(r^2)]`
`=(-1)/(4piepsilon_0) P cos theta(d)/(dr)((1)/(r^2))=-(1)/(4piepsilon_0)Pcos theta(-(2)/(r^3))`
`Er =-(1)/(4piepsilon_0)(2pcostheta)/(r^3)` तथा `E_(0)=-(1)/(r ) (del v)/(del theta)=-(1)/(r ) (del)/(del theta) ((1)/(4piepsilon_(0))(Pcos theta)/(r^2))`
`=-(1)/(4piepsilon_0)(P)/(r^3)((d cos theta)/(d theta))=-(1)/(4piepsilon_0)(P)/(r^3)(-sintheta)`
`therefore E_(theta)=(1)/(4piepsilon_0)(Psintheta)/(r^3)`
`E=sqrt(Er^(2)+E_(theta))=(1)/(4piepsilon_0)(P)/(r^3)(sqrt(4cos^(2)theta+sin^(2)theta)) `
`E=(1)/(4piepsilon_0)(P)/(r^3)sqrt(1+3cos^(2)theta)`

