Home
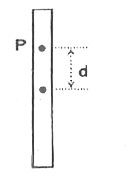
Class 12
PHYSICS
A pendulum is formed by pivoting a long ...

A pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.

The time period of this pendulum when d = L/2 will be

A

`2pi sqrt((2l)/(3g))`

B

`2pi sqrt((3l)/(2g))`

C

`4pi sqrt((l)/(3g))`

D

`(2pi)/(3) sqrt((2l)/(g))`

Text Solution

Verified by Experts

The correct Answer is:
A
Promotional Banner

Topper's Solved these Questions

  • SIMPLE HARMONIC MOTION

    FIITJEE|Exercise Assertion Reason type|1 Videos

  • SIMPLE HARMONIC MOTION

    FIITJEE|Exercise Numerical Based Questions|6 Videos

  • SIMPLE HARMONIC MOTION

    FIITJEE|Exercise Solved Problems (Objective)|16 Videos

  • SEMICONDUCTOR AND DEVICE

    FIITJEE|Exercise SOLVED PROBLEMS Objective: Level-I|20 Videos

  • TEST PAPERS

    FIITJEE|Exercise PHYSICS|747 Videos

Similar Questions

Explore conceptually related problems

A pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown. Time period will be minimum when d is equal to

A pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown. As d changes from L/2 to zero. Time period

A thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is

Two uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

The moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is

The moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L//3 from one of its ends and perpendicular to the rod is

Two identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is

Knowledge Check

  • A pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown. Time period will be minimum when d is equal to

    A
    `(L)/(sqrt12)`
    B
    `(L)/(sqrt6)`
    C
    `L//4`
    D
    `L//2`

  • A pendulum is formed by pivotting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown. As d changes from L/2 to zero

    A
    Time period increases continuously
    B
    Time period decreases continuously
    C
    Time period first increases then decrease
    D
    Time period first decreases then increase

  • A pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown. As d changes from L/2 to zero. Time period

    A
    increases continuously
    B
    decreases continuously
    C
    first increases then decrease
    D
    first decreases then increase
    • FIITJEE-SIMPLE HARMONIC MOTION-COMPREHENSION
    1. A pendulum is formed by pivoting a long thin rod of length L and mass ...

      Text Solution

      |

    2. A pendulum is formed by pivoting a long thin rod of length L and mass ...

      Text Solution

      |

    3. A pendulum is formed by pivoting a long thin rod of length L and mass ...

      Text Solution

      |

    4. A horizontal spring block system executes SHM with ampitude A = 10 cm ...

      Text Solution

      |

    5. A horizontal spring block system executes SHM with ampitude A = 10 cm ...

      Text Solution

      |

    6. A horizontal spring block system executes SHM with amplitude A = 10 cm...

      Text Solution

      |

    7. A horizontal spring block system executes SHM with amplitude A = 10 cm...

      Text Solution

      |

    8. A device used to print large maps, drawings, graphs, etc is known as p...

      Text Solution

      |

    9. A device used to print large maps, drawings, graphs, etc is known as p...

      Text Solution

      |

    10. A device used to print large maps, drawings, graphs, etc is known as p...

      Text Solution

      |

    11. The is an arrangement of pulleys as shown in figure. All the pulley ar...

      Text Solution

      |

    12. The is an arrangement of pulleys as shown in figure. All the pulley ar...

      Text Solution

      |

    13. The is an arrangement of pulleys as shown in figure. All the pulley ar...

      Text Solution

      |

    14. Two identical blocks P and Q have mass m each. They are attached to tw...

      Text Solution

      |

    15. Two identical blocks P and Q have mass m each. They are attached to tw...

      Text Solution

      |

    16. A pendulum is formed by pivotting a long thin rod of length L and mass...

      Text Solution

      |

    17. A pendulum is formed by pivotting a long thin rod of length L and mass...

      Text Solution

      |