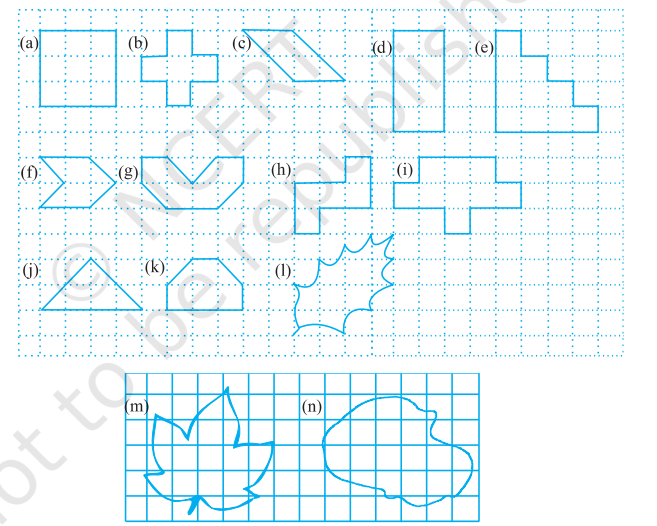
1. Find the areas of the following figures by counting square:
1. Find the areas of the following figures by counting square:


Text Solution
Verified by Experts
(a)We know that area of 1 square = 1 sq. unit
Now, the total number of squares in the figure = 9
Area of 9 squares `= 9 xx 1 `sq. unit
= 9 sq. units.
Therefore, the area of the given figure is 9 sq. units.
(b)There are 5 squares in the given figure.
So, Area of 5 squares `= 5 xx 1` sq. unit
= 5 sq. units
Therefore, the area of the figure is 5 sq. units
(c)There are 2 complete squares and 4 half squares in the figure.
So, Area of the figure =` 2 xx 1 + 4 xx 1/2 = 2 + 2` sq. units= 4 sq. units
Thus, the area of the given figure is 4 sq. units.
`(d)`There are 8 squares in the figure.
So, the area of the figure `= 8 xx 1` sq. unit
= 8 sq. units.
Therefore, the area of the given figure is 8 sq. units
(e)There are 10 squares in the figure.
So, the area of the figure` = 10 xx 1` sq. unit `= 10` sq units.
Thus, the area of the figure is 10 sq. units
(f)There are` 2 `complete squares and` 4 `half squares in the figure.
So, Area of the figure` = (2 xx 1 + 4 xx 1/2)`
`= (2 + 2)` sq units= 4 sq. units.
Thus, area of the given figure is` 4 `sq. units
(g)There are `4 `complete squares and` 4` half squares in the figure.
So, Area of the given figure` = (4 xx 1 + 4 xx 1/2)`
`= (4 + 2)` sq. units
`= 6` sq. units.
Therefore, the area of the given figure is 6 sq. units
(h)There are` 5 `squares in the figure.
So, Area of the figure` = 5 xx 1` sq. unit
`= 5 `sq. units.
Thus, the area of the given figure is 5 sq. units.
(i)There are` 9 `squares in the figure.
So, Area of the figure` = 9 xx 1= 9 `sq. units
Thus, the area of the given figure is 9 sq. units
(j)There are 2 complete squares and 4 half squares in the figure.
So, Area of the figure` =(2 xx1 + 4 xx 1/2)` sq. units= (2 + 2) sq. units
= 4 sq. units.
Thus, the area of the figure is 4 sq. units.
(k)There are` 4` complete squares and` 2` half squares in the figure.
So, Area of the figure` = (4 xx 1 + 2 × 1/2)` sq. units
`= (4 + 1) `sq. units
`= 5 `sq. units
Thus, the area of the figure is `5` sq. units
(l)There are` 4` complete squares, `3` greater than half squares and` 2` halfnsquares in the figure.
So, Area of the figure` = (4 xx 1 + 3 xx 1 + 2 × 1/2) `sq units
`= (4 + 3 + 1)` sq units
= 8 sq units
(m)There are` 6` complete squares and` 8 `greater than half squares in the figure.
So, Area of the figure` = (6 xx 1 + 8 xx 1)` sq units
`= 6 + 8` sq. units
`= 14` sq. units
(n)There are` 9 `complete squares and` 9` greater than half squares in the figure.
So, Area of the figure` = (9 xx 1 + 9 xx 1)` sq units
`=(9 + 9)` sq units
`= 18 `sq units.
Now, the total number of squares in the figure = 9
Area of 9 squares `= 9 xx 1 `sq. unit
= 9 sq. units.
Therefore, the area of the given figure is 9 sq. units.
(b)There are 5 squares in the given figure.
So, Area of 5 squares `= 5 xx 1` sq. unit
= 5 sq. units
Therefore, the area of the figure is 5 sq. units
(c)There are 2 complete squares and 4 half squares in the figure.
So, Area of the figure =` 2 xx 1 + 4 xx 1/2 = 2 + 2` sq. units= 4 sq. units
Thus, the area of the given figure is 4 sq. units.
`(d)`There are 8 squares in the figure.
So, the area of the figure `= 8 xx 1` sq. unit
= 8 sq. units.
Therefore, the area of the given figure is 8 sq. units
(e)There are 10 squares in the figure.
So, the area of the figure` = 10 xx 1` sq. unit `= 10` sq units.
Thus, the area of the figure is 10 sq. units
(f)There are` 2 `complete squares and` 4 `half squares in the figure.
So, Area of the figure` = (2 xx 1 + 4 xx 1/2)`
`= (2 + 2)` sq units= 4 sq. units.
Thus, area of the given figure is` 4 `sq. units
(g)There are `4 `complete squares and` 4` half squares in the figure.
So, Area of the given figure` = (4 xx 1 + 4 xx 1/2)`
`= (4 + 2)` sq. units
`= 6` sq. units.
Therefore, the area of the given figure is 6 sq. units
(h)There are` 5 `squares in the figure.
So, Area of the figure` = 5 xx 1` sq. unit
`= 5 `sq. units.
Thus, the area of the given figure is 5 sq. units.
(i)There are` 9 `squares in the figure.
So, Area of the figure` = 9 xx 1= 9 `sq. units
Thus, the area of the given figure is 9 sq. units
(j)There are 2 complete squares and 4 half squares in the figure.
So, Area of the figure` =(2 xx1 + 4 xx 1/2)` sq. units= (2 + 2) sq. units
= 4 sq. units.
Thus, the area of the figure is 4 sq. units.
(k)There are` 4` complete squares and` 2` half squares in the figure.
So, Area of the figure` = (4 xx 1 + 2 × 1/2)` sq. units
`= (4 + 1) `sq. units
`= 5 `sq. units
Thus, the area of the figure is `5` sq. units
(l)There are` 4` complete squares, `3` greater than half squares and` 2` halfnsquares in the figure.
So, Area of the figure` = (4 xx 1 + 3 xx 1 + 2 × 1/2) `sq units
`= (4 + 3 + 1)` sq units
= 8 sq units
(m)There are` 6` complete squares and` 8 `greater than half squares in the figure.
So, Area of the figure` = (6 xx 1 + 8 xx 1)` sq units
`= 6 + 8` sq. units
`= 14` sq. units
(n)There are` 9 `complete squares and` 9` greater than half squares in the figure.
So, Area of the figure` = (9 xx 1 + 9 xx 1)` sq units
`=(9 + 9)` sq units
`= 18 `sq units.
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
Find the area of the following figure
Find the area of the following figures.
Find the area of the following figure by counting squares.
Find the area of the following figure by counting squares.
Find the area of the following figure by using a squared paper.
Find the areas of the following figures (All measurements are in metre)
Find the area of the following regular hexagon Figure
Find the umber of squares in the following figure.
Find the number of squares in the following figure.
Find the number of squares in the following figure .