Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTRIC CHARGES AND FIELDS
NEW JOYTHI PUBLICATION|Exercise Previous Year Questions|3 VideosELECTRIC CHARGES AND FIELDS
NEW JOYTHI PUBLICATION|Exercise Competitive Exam Corner|20 VideosELECTRIC CHARGES AND FIELDS
NEW JOYTHI PUBLICATION|Exercise Solution To Exercises From NCERT Text|26 VideosDUAL NATURE OF RADIATION AND MATTER
NEW JOYTHI PUBLICATION|Exercise COMPETITIVE EXAM CORNER|15 VideosELECTROMAGNETIC INDUCTION
NEW JOYTHI PUBLICATION|Exercise COMPETITIVE EXAM CORNER|13 Videos
Similar Questions
Explore conceptually related problems
NEW JOYTHI PUBLICATION-ELECTRIC CHARGES AND FIELDS -Evaluation Questions And Answers
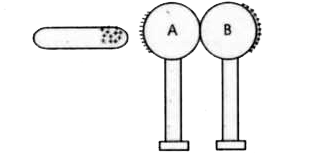
- A glass rod rubbed with silk is brought close to two uncharged spheres...
Text Solution
|
- Although ordinary rubber is an insulator, the special rubber tyres of ...
Text Solution
|
- Vehicles carrying inflammable material usually have metallic ropes tou...
Text Solution
|
- Is Coulomb a very big unit of charge?
Text Solution
|
- The electric field can be studied in terms of electric field intensity...
Text Solution
|
- Show mathematically that the electric field strength due to a short el...
Text Solution
|
- What is the total force acting on the dipole placed in a uniform elect...
Text Solution
|
- What is the effect of keeping the dipole in the field?
Text Solution
|
- What happens if the field is not uniform?
Text Solution
|
- The following four insulating spheres contain magnet, dipole, proton a...
Text Solution
|
- How does the electric field (E) vary with distance (r) in the followin...
Text Solution
|
- Give the expression for the time-period of oscillation of an electric ...
Text Solution
|