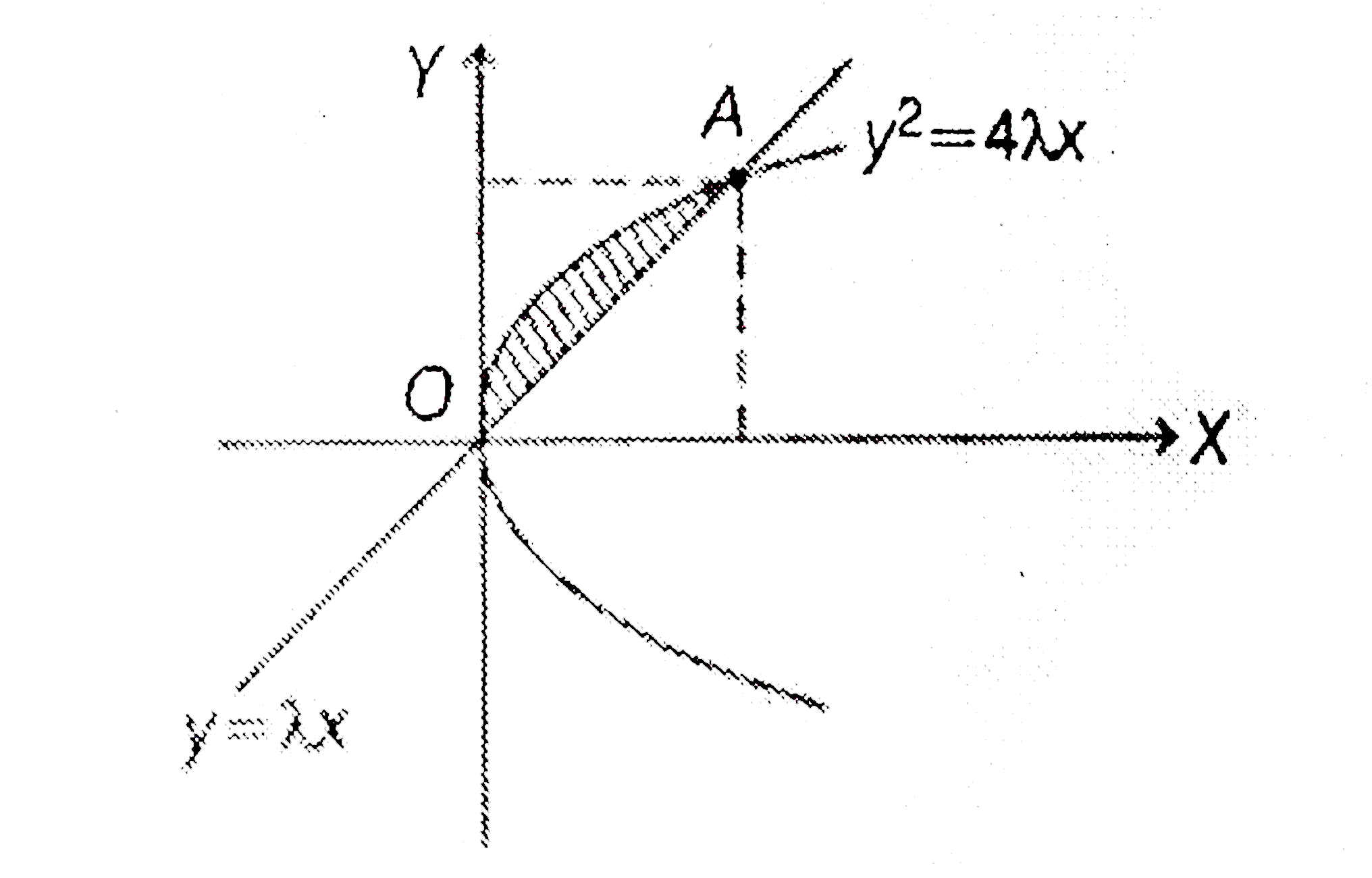A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- If the area (in sq. units) bounded by the parabola y^(2) = 4 lambda x ...
Text Solution
|
- If (x+y)^(2)=2(x^(2)+y^(2)) and (x-y+lambda)^(2)=4,lambda>0 then lambd...
Text Solution
|
- If the equation lambda x^(2)+4xy+y^(2)+lambda x+3y+2=0 represent a par...
Text Solution
|
- If the following equations x+y-3=0,(1+lambda)x+(2+lambda)y-8=0,x-(1+la...
Text Solution
|
- the lines (x+3)/(2)=(y)/(1)=(z-4)/(3) and (x)/(lambda)=(y-1)/(lambda+1...
Text Solution
|
- The circle x^(2)+y^(2)+4 lambda x=0 which lambda in R touches the para...
Text Solution
|
- If (x+y)^(2)=2(x^(2)+y^(2)) and (xy+lambda)^(2)=4,lambda>0, then lambd...
Text Solution
|
- For any lambda in R, the locus x^(2)+y^(2)-2 lambda x-2 lambda y+lambd...
Text Solution
|
- if the area enclosed by the curves y^(2)=4lamdax and y=lamdax is (1)/(...
Text Solution
|