Text Solution
Verified by Experts
|
Topper's Solved these Questions
CBSE EXAMINATION PAPER 2020 (SOLVED)
U-LIKE SERIES|Exercise SECTION C|11 VideosView PlaylistCBSE EXAMINATION PAPER 2020
U-LIKE SERIES|Exercise SECTION D|12 VideosView PlaylistCBSE EXAMINATION PAPER 2020 (SOLVED)
U-LIKE SERIES|Exercise SECTION - D|6 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
U-LIKE SERIES-CBSE EXAMINATION PAPER 2020 (SOLVED)-SECTION D
- Define the term 'focal length ofa mirror. With the help of a ray diagr...
Text Solution
|
Play - Calculate the angle of emergence (e) of the ray of light incident norm...
Text Solution
|
Play - Define the term 'resolving power of a telescope'. How will the resolvi...
Text Solution
|
Play - A screen is placed 80 cm from an object. The image of the object on th...
Text Solution
|
Play - Show that an ideal inductor does not dissipate power in an ac circuit.
Text Solution
|
Play - The variation of inductive reactance (X(L)) of an inductor with the fr...
Text Solution
|
Play - A conductor of length T'is rotated about one of its ends at a constant...
Text Solution
|
Play - Two concentric circular loops of radius 1 cm and 20 cm are placed coax...
Text Solution
|
Play - Write two important characteristics of equipotential surfaces.
Text Solution
|
Play - A thin circular ring of radius r is charged uniformly so that its line...
Text Solution
|
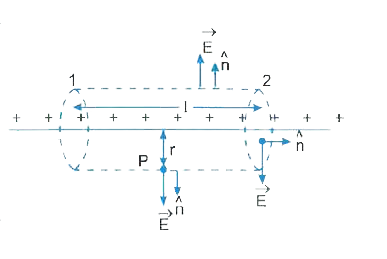
Play - State Gauss's law on electrostatics and derive an expression for the e...
Text Solution
|
Playing Now