Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
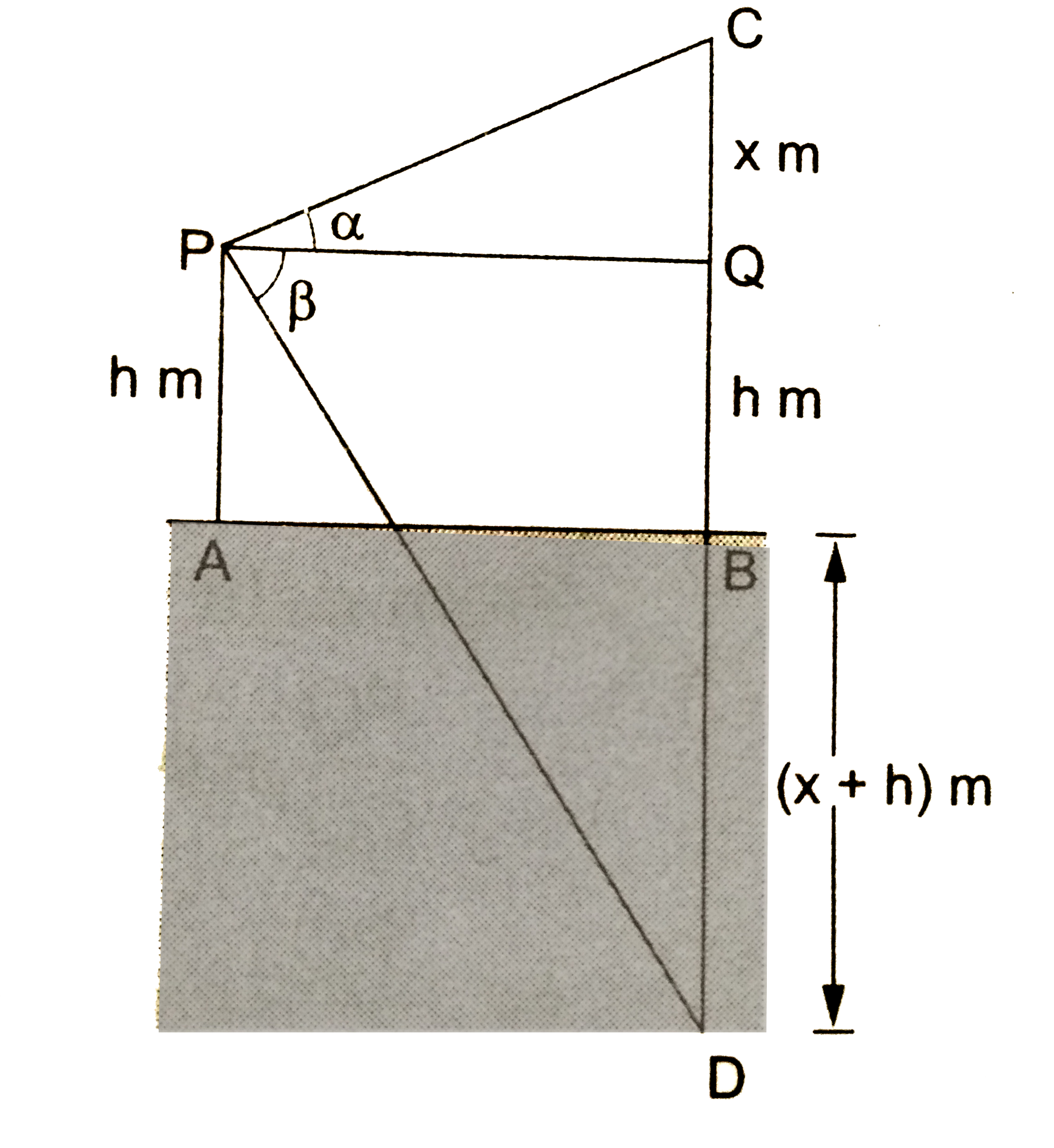
- If the angle of elevation of a cloud from a point h metres above a lak...
Text Solution
|
- The angle of elevation of a cloud from a point h metre above a lake is...
Text Solution
|
- The angle of elevation of a cloud from a point 'h' metres above a lake...
Text Solution
|
- एक झील से h मीटर ऊँचाई पर बादलों का उन्नयन कोण alpha है तथा झील में ...
Text Solution
|
- From a point a metres above a lake the angle of elevation of a cloud i...
Text Solution
|
- The angle of elevation of a cloud from a point h mt. above is theta^@ ...
Text Solution
|
- The angle of elevation of a cloud from a point h metres above a lake i...
Text Solution
|
- The angle of elevation of a cloud from a point h mt above the surface ...
Text Solution
|
- The angle of elevation of a cloud from a point h metres above the surf...
Text Solution
|