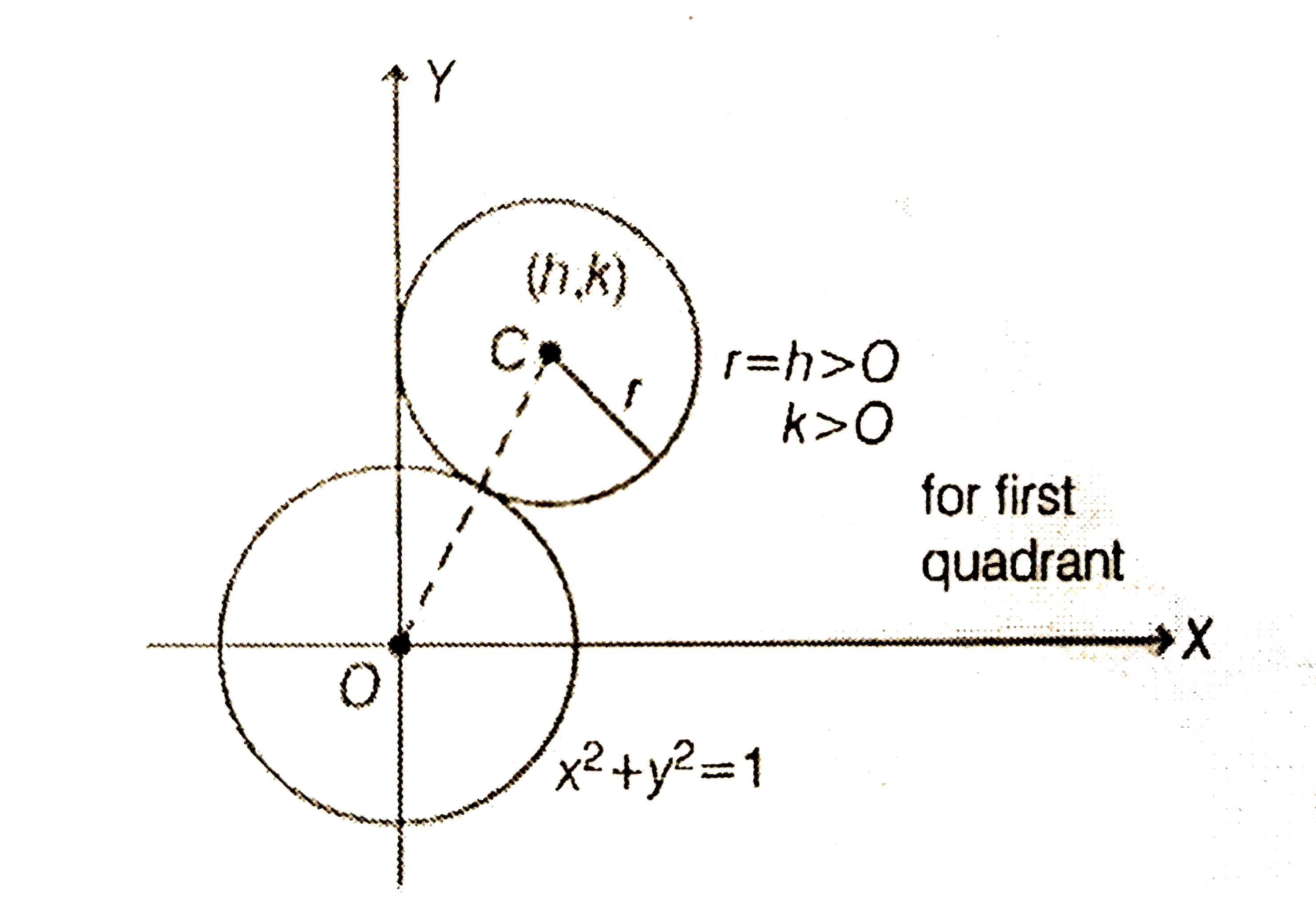A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
CIRCLE
IIT JEE PREVIOUS YEAR|Exercise Topic 4 Fill in the blanks|4 VideosView PlaylistCIRCLE
IIT JEE PREVIOUS YEAR|Exercise Topic 4 Analytical & Descriptive Questions|7 VideosView PlaylistCIRCLE
IIT JEE PREVIOUS YEAR|Exercise Topic 3 Integer Answer Type Question|1 VideosView PlaylistBINOMIAL THEOREM
IIT JEE PREVIOUS YEAR|Exercise Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )|8 VideosView PlaylistCOMPLEX NUMBERS
IIT JEE PREVIOUS YEAR|Exercise TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)|1 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
IIT JEE PREVIOUS YEAR-CIRCLE-Topic 4 Radical Axis and Family of Circle
- The locus of the centres of the circles, which touch the circle, x^(2...
02:37
|
Playing Now - The line x = y touches a circle at the point (1, 1). If the circle al...
03:34
|
Play - Two circle of equal radii are intersect at (0, 1) and (0, ?1), and the...
04:56
|
Play - 3 circles of radii a,b,c (a<b<c) touch each other externally and have ...
04:59
|
Play - The circle passing through (1, -2) and touching the axis of x at (3...
04:16
|
Play - The circle passing through the point (-1,0) and touching the y-axis at...
03:06
|
Play - The locus of the centres of circles which touches (y-1)^(2)+x^(2)=1 ex...
05:08
|
Play - If two distinct chords, drawn from the point (p, q) on the circle x^2+...
03:47
|
Play - The locus of the centre of a circle which touches externally the circl...
04:03
|
Play - A circle passes through (0,0) and (1, 0) and touches the circle x^2 + ...
03:28
|
Play - Show that the equation of the circle passing through (1, 1) and the ...
02:28
|
Play - Two circle x^2+y^2=6 and x^2+y^2-6x+8=0 are given. Then the equation o...
02:37
|
Play