Text Solution
Verified by Experts
|
Topper's Solved these Questions
CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)
U-LIKE SERIES|Exercise SECTION D|6 VideosView PlaylistCBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)
U-LIKE SERIES|Exercise SECTION B|9 VideosView PlaylistCBSE EXAMINATION PAPER 2020 (SOLVED)
U-LIKE SERIES|Exercise SECTION - D|6 VideosView PlaylistCURRENT ELECTRICITY
U-LIKE SERIES|Exercise SELF ASSESSMENT TEST (SECTION C )|3 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
U-LIKE SERIES-CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)-SECTION C
- State working principle of potentiometer. Explain how the balance poin...
Text Solution
|
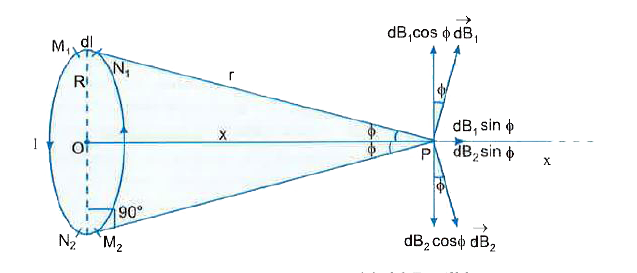
Play - Using Biot - Savart's law, derive an expression for magnetic field at...
Text Solution
|
Playing Now - Obtain the resonant frequency and Q - factor of a series LCR circuit w...
Text Solution
|
Play - State the conditions of total internal reflection. Refractive indices ...
Text Solution
|
Play - Define resolving power of an astronomical refracting telescope and wri...
Text Solution
|
Play - Write the basic assumptions used in the derivation of lens- maker's fo...
Text Solution
|
Play - Show that ""(92)^(238)U cannot spontaneosly emit a proton. Given : "...
Text Solution
|
Play - Suggest an ideal to convert a full wave bridge rectifier to a half wav...
Text Solution
|
Play